FluidStu
- 25
- 3
When considering the Wave equation subject to initial conditions as follows…
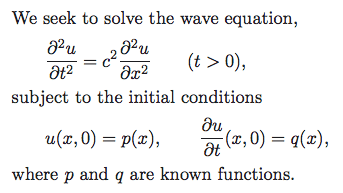
…then D'Alembert's solution is given by (where c is wave speed):
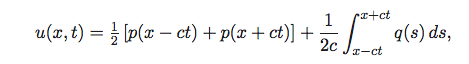
I'd like to understand physically how this formula allows us to know the value of u (where u is the height of the wave, say) at some point (x0,t0). With relation to the diagram below, I understand that the height u is constant along the characteristic lines, and that moving along these characteristic lines in the x-t plane is how the wave crest (at height u) would propagate forwards/backwards in time.
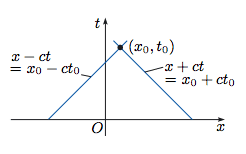
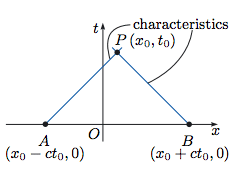
So, referring to D'Alembert's formula above, says that the height of the wave is given by:
The region between the two possible starting points is called the domain of dependence – meaning that the height of the wave at the point (x0,t0) depends only on initial data specified within this range. Why is there a domain of dependence? Why do conditions in the region between these two points influence the height at (x0,t0),? It would seem that the height at (x0,t0) would depend only on the conditions at the two starting points.
…then D'Alembert's solution is given by (where c is wave speed):
I'd like to understand physically how this formula allows us to know the value of u (where u is the height of the wave, say) at some point (x0,t0). With relation to the diagram below, I understand that the height u is constant along the characteristic lines, and that moving along these characteristic lines in the x-t plane is how the wave crest (at height u) would propagate forwards/backwards in time.
So, referring to D'Alembert's formula above, says that the height of the wave is given by:
- The average height u of the wave between the two possible starting positions of the wave (the two intersections of x-axis).
- The average rate of increase of the height of the wave between the two possible starting points.
The region between the two possible starting points is called the domain of dependence – meaning that the height of the wave at the point (x0,t0) depends only on initial data specified within this range. Why is there a domain of dependence? Why do conditions in the region between these two points influence the height at (x0,t0),? It would seem that the height at (x0,t0) would depend only on the conditions at the two starting points.