Dimani4
- 50
- 0
Hi,
I have a question in definition of reflection/transmission coefficients in TE/TM modes.
Let's see TE polarization case.
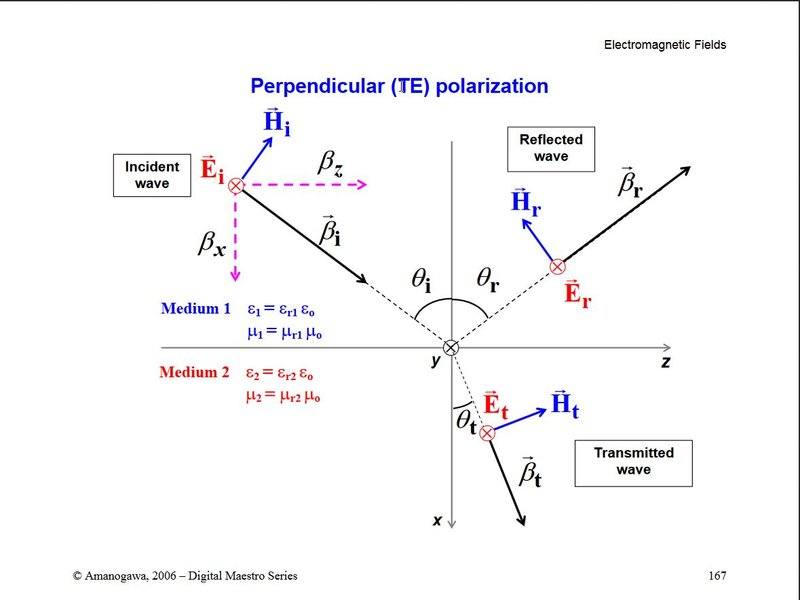
The reflection coefficient for the magnetic field is defined as:
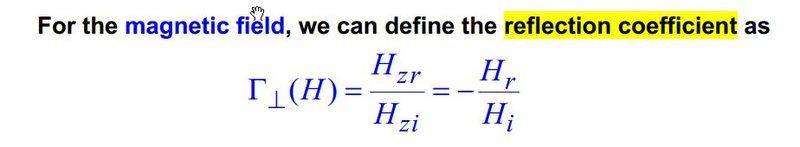
However the transmission coefficient for the magnetic field is defined as:

Now, let's see the TM mode.
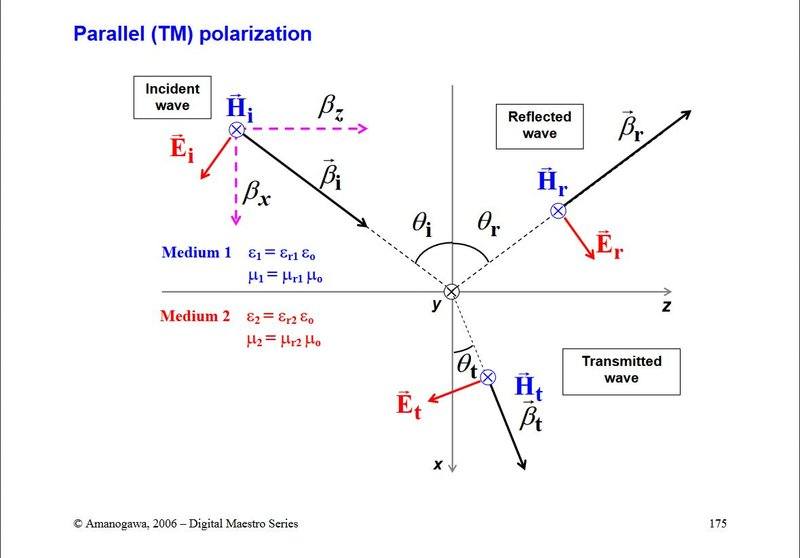
Here, transmission coefficient for electric field is defined as:

And the reflection coefficient is defined as;

My question is: why the reflection coefficient is defined the only by the parallel component of the magnetic (Hz for TE) and electric field (Ez for TM) but the transmission coefficient is defined by the whole component (Et/Ei or Ht/Hi of the electric/magnetic field?
Thank you.
The pictures are taken from the attached pdf file (EM13).
I have a question in definition of reflection/transmission coefficients in TE/TM modes.
Let's see TE polarization case.
The reflection coefficient for the magnetic field is defined as:
However the transmission coefficient for the magnetic field is defined as:
Now, let's see the TM mode.
Here, transmission coefficient for electric field is defined as:
And the reflection coefficient is defined as;
My question is: why the reflection coefficient is defined the only by the parallel component of the magnetic (Hz for TE) and electric field (Ez for TM) but the transmission coefficient is defined by the whole component (Et/Ei or Ht/Hi of the electric/magnetic field?
Thank you.
The pictures are taken from the attached pdf file (EM13).

