- #1
Jeronimus
- 287
- 9
Following scenario:
A rocket measuring 10 lightseconds in length accelerates near instantaneously to v=0.4c. Pre-acceleration two clocks placed at the endpoints of the rocket were synced.
What will be the time difference between the two clocks post acceleration?
I tried to figure it out, using two x-t diagrams, drawing the worldlines of the rocket's endpoints (green lines) as i would imagine them.
Considering the innacuracy of the drawing, my rough estimate is that the time difference will be slightly over 4 seconds. Did i get it right?
Here are the x-t diagrams
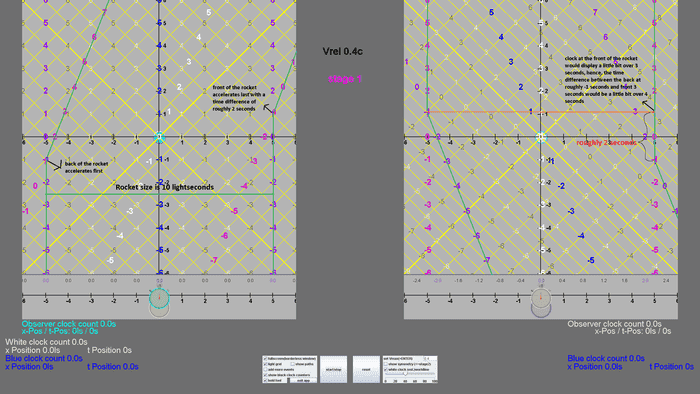
edit: Also, is the time difference between the two clocks post acceleration decided only by the final velocity or does the "type" of acceleration (faster/slower) matter?
A rocket measuring 10 lightseconds in length accelerates near instantaneously to v=0.4c. Pre-acceleration two clocks placed at the endpoints of the rocket were synced.
What will be the time difference between the two clocks post acceleration?
I tried to figure it out, using two x-t diagrams, drawing the worldlines of the rocket's endpoints (green lines) as i would imagine them.
Considering the innacuracy of the drawing, my rough estimate is that the time difference will be slightly over 4 seconds. Did i get it right?
Here are the x-t diagrams
edit: Also, is the time difference between the two clocks post acceleration decided only by the final velocity or does the "type" of acceleration (faster/slower) matter?
Last edited: