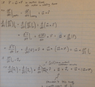Derivation of acceleration in rotating coordinates

[TheCanadian]

I was just trying to write out the derivation for an object's trajectory from an inertial coordinate system if the object is rotating in another coordinate system (e.g. finding Coriolis, centrifugal acceleration). I seem to have gotten something close to what I was looking for, but after checking the formula, it shows a coefficient of 2 on the Coriolis term online, yet that is not what I derived. I have let the Euler acceleration = 0 by letting $\frac {d\vec{\omega}}{dt} = 0$, but by doing this am I losing a term? Have I done anything wrong with my derivation in general?

 

[Mercy]

In the last line where you cancel out $$ \frac {d}{dt} (\omega x r) $$

Use the product rule on this term to obtain $$ (\dot{\omega} x r) + (\omega x \dot{r}) $$

the former term is the one that you throw away and the latter, combined with the last term in your second to last line, form $$2\omega x v_r $$

hope that makes sense :)

 

[TheCanadian]

In the last line where you cancel out $$ \frac {d}{dt} (\omega x r) $$

Use the product rule on this term to obtain $$ (\dot{\omega} x r) + (\omega x \dot{r}) $$

the former term is the one that you throw away and the latter, combined with the last term in your second to last line, form $$2\omega x v_r $$

hope that makes sense :)

Thank you for the response.

The only thing is, that term is strictly $\frac {d(\omega)}{dt} \times r$ since it was derived from using the product rule earlier. In case I'm missing something, it is only the time derivative of $\omega$ in the last line, and not both cross product of both terms (i.e. not the time derivative of $\omega \times r$).

 

[Mercy]

Then did you forget to include the last term in the second to last line? It looks like it disappeared

 

[TheCanadian]

Then did you forget to include the last term in the second to last line? It looks like it disappeared

Sorry for the confusion since I rearranged some terms from the second last to last line. Essentially all I did was state that $\frac{d\vec{r}}{dt}_r = \vec{v}_r$ and so the $\omega \times \frac{d\vec{r}}{dt}_r$ term just appears as $\omega \times \vec{v}_r$. Sorry for the slight sloppiness in that line, but I believe the math works out fine.

 

[Mercy]

$$ v_{fix} = \frac{dr}{dt}_{rot} + (\omega x r) $$

$$ \big( \frac{dv}{dt} \big)_{fix} = \big( \frac{dv_{rot}}{dt} \big)_{fix} + (\dot{\omega} x r) + \omega x \big( \frac{dr}{dt} \big)_{fix} $$

$$a_f = a_r + (\omega x v_r) + (\dot{\omega} x r) + (\omega x (\omega x r) ) + (\omega x v_r) $$

$$ a_f = a_r + (\dot{\omega} x r) + (\omega x (\omega x r) ) + 2(\omega x v_r) $$
subscripts: f = fixed frame, r = rotating frame

Here's a quick derivation, you just have to expand the two "fix" terms in the second line properly and then everything should work out. I'd explain a bit more but I need to go catch the bus home :) Hope you can compare to yours and figure out where the mistake is. Cheers

 

[TheCanadian]

$$ v_{fix} = \frac{dr}{dt}_{rot} + (\omega x r) $$

$$ \big( \frac{dv}{dt} \big)_{fix} = \big( \frac{dv_{rot}}{dt} \big)_{fix} + (\dot{\omega} x r) + \omega x \big( \frac{dr}{dt} \big)_{fix} $$

$$a_f = a_r + (\omega x v_r) + (\dot{\omega} x r) + (\omega x (\omega x r) ) + (\omega x v_r) $$

$$ a_f = a_r + (\dot{\omega} x r) + (\omega x (\omega x r) ) + 2(\omega x v_r) $$
subscripts: f = fixed frame, r = rotating frame

Here's a quick derivation, you just have to expand the two "fix" terms in the second line properly and then everything should work out. I'd explain a bit more but I need to go catch the bus home :) Hope you can compare to yours and figure out where the mistake is. Cheers

Thank you for the derivation. I think the one part I am not quite catching is $\big( \frac{dv_{rot}}{dt} \big)_{fix}$.

How is that expression equal to $a_r + (\dot{\omega} x r)$? Isn't it simply $a_r$?

 

[DrGreg]

$$ v_{fix} = \frac{dr}{dt}_{rot} + (\omega x r) $$

By the way, the way to do vector products in LATEX is to use "\times" instead of "x":$$ v_{fix} = \frac{dr}{dt}_{rot} + \omega \times r$$

 

[Mercy]

By the way, the way to do vector products in LATEX is to use "\times" instead of "x":$$ v_{fix} = \frac{dr}{dt}_{rot} + \omega \times r$$

haha thank you it was bugging me that I couldn't figure it out :)

 

[TheCanadian]

$$ v_{fix} = \frac{dr}{dt}_{rot} + (\omega x r) $$

$$ \big( \frac{dv}{dt} \big)_{fix} = \big( \frac{dv_{rot}}{dt} \big)_{fix} + (\dot{\omega} x r) + \omega x \big( \frac{dr}{dt} \big)_{fix} $$

$$a_f = a_r + (\omega x v_r) + (\dot{\omega} x r) + (\omega x (\omega x r) ) + (\omega x v_r) $$

$$ a_f = a_r + (\dot{\omega} x r) + (\omega x (\omega x r) ) + 2(\omega x v_r) $$
subscripts: f = fixed frame, r = rotating frame

Here's a quick derivation, you just have to expand the two "fix" terms in the second line properly and then everything should work out. I'd explain a bit more but I need to go catch the bus home :) Hope you can compare to yours and figure out where the mistake is. Cheers

Also, just to clarify, did you mean to state: $\big( \frac{dv_{rot}}{dt} \big)_{fix} = a_r + (\dot{\omega} \times r)$ or did I misinterpret your post?

 

[Mercy]

No, what I wrote is what is in my textbook (Thorton/Marion pg 389 - 392).

Fixed frame quantities expand this way:

$$ \big( \frac{dr}{dt} \big)_{fixed} = \big( \frac{dr}{dt} \big)_{rot}+ (\omega \times r) $$

So from the second line:

$$ \big( \frac{dv_{rot}}{dt} \big)_{fixed} =a_r+ (\omega \times v_r) $$

$$ \omega \times \big( \frac{dr}{dt} \big)_{fixed} = (\omega \times v_r) + \omega \times (\omega \times r)) $$

So from expanding the second line in my earlier post, you can see that two $$ (\omega \times v_r) $$ terms come out.

 

[Mercy]

The $$ (\dot{\omega} \times r) $$ term comes from the product rule from the time derivative of the last term in the first line.

 

[TheCanadian]

No, what I wrote is what is in my textbook (Thorton/Marion pg 389 - 392).

Fixed frame quantities expand this way:

$$ \big( \frac{d}{dt} \big)_{fixed} = \big( \frac{d}{dt} \big)_{rot}+ (\omega \times ) $$

Okay, that seems to be where my confusion arose. But is that true for higher order terms (e.g. acceleration, jerk, etc.)?

 

[Mercy]

I would assume so, you would just be taking another set of time derivatives, although I'm not 100% sure on that.

 

[TheCanadian]

I would assume so, you would just be taking another set of time derivatives, although I'm not 100% sure on that.

Just checked Marion (thank you for the reference) and it helped a lot. It does in fact state that you can use any vector in that expression to go from fixed to a rotating frame...just trying to intuitively see that now. When that vector itself changes with time, it (to me at least) is not very easy to understand. But considering just any arbitrary vector, this seems to make sense. It's almost like a first-order of time perturbation to the vector, and it seems independent of the vector itself.