Derivation of an Equivalent Spring Constant

[Saladsamurai]

Okay. I have been at this for two nights now. I want to derive, step by step, the equivalent spring constant of a Beam cantilevered at both ends with a loading at its center.

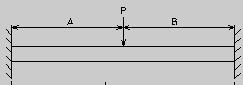
Here is a schematic with A=B=L/2

Now I would like to use superposition to find the deflection at L/2 due to the loading. I know there are tables out there, but I want to "derive" this. (I know that I am not really deriving it since I am using superposition and tables...but bear with me).
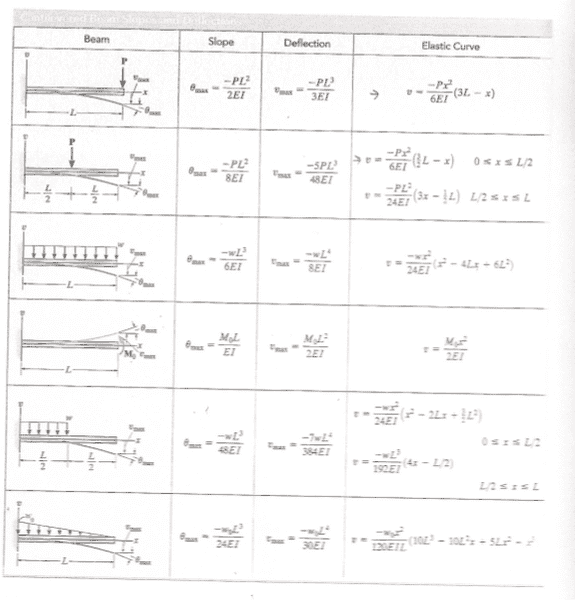
Here are the equations I have at my disposal. Calling them from top to bottom 1-6,
I think that 1, 2, and 4 will prove the most useful, but I could be wrong.

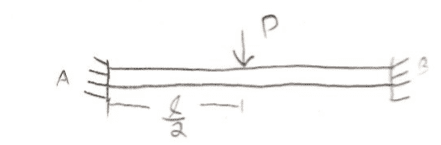
Now, if I replace the fixed end at the right with its reaction force and moment I have:

=

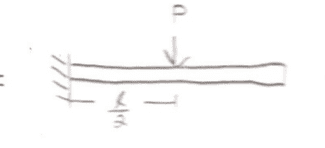
1

+

2

+

3

 

[Saladsamurai]

From inspection we can see automatically that the reaction forces at both ends are given by:

R_A=R_B=P/2

The moments are giving me trouble though. I believe M=(1/12)*PL according to my mechanics book. But I could be wrong.

Can someone confirm that? And that the direction of M_B is indeed clockwise?

 

[FredGarvin]

See if this helps...it's from the bible according to Roark's. I have done this problem a long time ago but I'd have to dig it up. This should be quicker by giving you something to shoot for. Notice the max deflection values at x=a.

 

[Rybose]

This problem difficult because you can't determine the reaction moments through equilibrium alone (statically indeterminate). Therefore you need to use information about the deflection to solve the problem.

With the symmetry of the problem you know:

y(0) = y(L) = 0

\frac{dy}{dx}_{x = 0} = \frac{dy}{dx}_{x = L/2} = \frac{dy}{dx}_{x = L} = 0

Split the problem into two parts. Integrate the equation to get y' and y. Use the 3 relevant boundary conditions to solve for the two integration constants and the reaction moment Ma.

M(x) = EI \frac{d^2y}{dx^2} = -M_{A} + \frac{P}{2}(x)

Good luck