- #1
Prockey
- 3
- 2
- TL;DR Summary
- Selection of a torsion spring to open a hinged lid
Hi,
I'm designing a small container with a spring loaded hollow rectangular lid. I want the lid to open when a button is pressed, so I have a torsion spring at the hinge. I want to know if the spring I selected is able to open the lid and also how long it would take to open 90°.
Below is a diagram of the hinge, spring and the center of gravity (COG) of the lid. The mass of the lid is 0.005 kg.
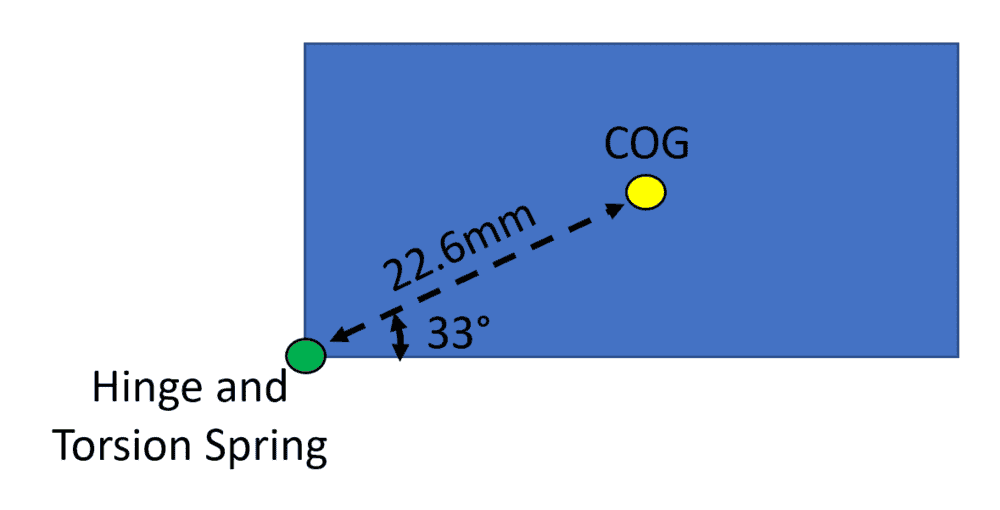
This is what I have so far:
Torque needed to open lid:
Torque = weight * distance to COG * Cos(33)
= 0.005 kg * 9.8 m/s^2 * 0.0226 m * 0.8386
= 0.0009 Nm
I'm going to design a custom spring, but for the sake of this question let's assume this torsion spring from McMaster which has a max torque of 0.117 in-lbs (0.0132 Nm).

Question #1: Since this spring is able to provide 0.0132 Nm and I only need 0.0009 Nm, the spring should work. Is this correct?
I also want to know how fast the lid will open in seconds given this spring.
I'm getting the center of gravity MoI from CAD, which I think I need:
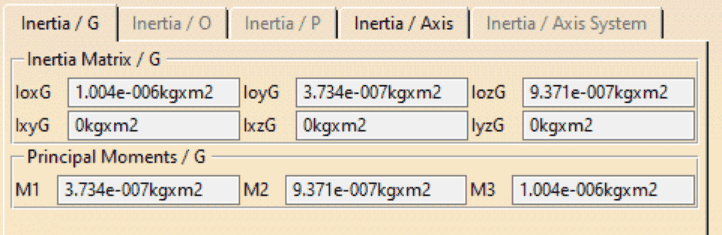
I know that: Torque = Moment of inertia * angular acceleration
So: Angular acceleration = Torque/MoI
Using the spring torque and the Z MoI:
Angular acceleration = 0.0132 Nm/9.371e-007kg*m2
= 14087 rad/s^2
Question #2: Is this correct? This 14087 rad/s^2 answer seems way too fast to me.
Question #3: How do I convert this angular acceleration to the number of seconds it will take the lid to open 90°? I would like it to open in less than 1 second.
Thank you for your time!
I'm designing a small container with a spring loaded hollow rectangular lid. I want the lid to open when a button is pressed, so I have a torsion spring at the hinge. I want to know if the spring I selected is able to open the lid and also how long it would take to open 90°.
Below is a diagram of the hinge, spring and the center of gravity (COG) of the lid. The mass of the lid is 0.005 kg.
This is what I have so far:
Torque needed to open lid:
Torque = weight * distance to COG * Cos(33)
= 0.005 kg * 9.8 m/s^2 * 0.0226 m * 0.8386
= 0.0009 Nm
I'm going to design a custom spring, but for the sake of this question let's assume this torsion spring from McMaster which has a max torque of 0.117 in-lbs (0.0132 Nm).
Question #1: Since this spring is able to provide 0.0132 Nm and I only need 0.0009 Nm, the spring should work. Is this correct?
I also want to know how fast the lid will open in seconds given this spring.
I'm getting the center of gravity MoI from CAD, which I think I need:
I know that: Torque = Moment of inertia * angular acceleration
So: Angular acceleration = Torque/MoI
Using the spring torque and the Z MoI:
Angular acceleration = 0.0132 Nm/9.371e-007kg*m2
= 14087 rad/s^2
Question #2: Is this correct? This 14087 rad/s^2 answer seems way too fast to me.
Question #3: How do I convert this angular acceleration to the number of seconds it will take the lid to open 90°? I would like it to open in less than 1 second.
Thank you for your time!
Last edited: