CAF123
Gold Member
- 2,918
- 87
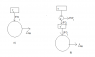
I have been reading about the derivation of Clausius' Inequality and there are a few things I do not understand. I have attached an image of the cycles.
B) shows one carnot engine performing work ##d W_i## per cycle and delivering heat ##d Q_i## per cycle. For ##T'## to remain unchanged, it spits out heat ##d Q_i## as well and this is considered as the source of heat of the principal engine represented by that large circle.
From the first law, ##\Delta W = Q = \sum_i d Q_i##, where ##i## runs from 1 to the number of operating carnot engines connected to the principal engine. My book says that necessarily ##\Delta W = Q \leq 0## otherwise we have a violation of Kelvin-Planck. This means that work is done on the system (I think this makes sense - ΔW was initially regarded as the work done by the engine, but if it is negative then this means work is done on the system by surroundings) and heat flows out of the system. A situation in which an amount of work entering a substance is completely converted into heat is allowed.
I just want to make sure I know what is going on here: Initially we consider the case where heat is flowing into the engine with an equal amount of work being done. This has to happen via the first law since there is no reservoir at a lower temperature with which the engine can spit out heat. This then implies a violation of KP unless we consider both W and Q to be negative, which reverses the physical picture of what was going on initially - work is now being done on the system and heat is flowing out of the engine into the reservoir.
The conclusion is that an engine taking in heat per cycle must always spit out some heat per cycle to a reservoir if it is to do work. Without this reservoir, it cannot exist.
Is this right? Many thanks.
B) shows one carnot engine performing work ##d W_i## per cycle and delivering heat ##d Q_i## per cycle. For ##T'## to remain unchanged, it spits out heat ##d Q_i## as well and this is considered as the source of heat of the principal engine represented by that large circle.
From the first law, ##\Delta W = Q = \sum_i d Q_i##, where ##i## runs from 1 to the number of operating carnot engines connected to the principal engine. My book says that necessarily ##\Delta W = Q \leq 0## otherwise we have a violation of Kelvin-Planck. This means that work is done on the system (I think this makes sense - ΔW was initially regarded as the work done by the engine, but if it is negative then this means work is done on the system by surroundings) and heat flows out of the system. A situation in which an amount of work entering a substance is completely converted into heat is allowed.
I just want to make sure I know what is going on here: Initially we consider the case where heat is flowing into the engine with an equal amount of work being done. This has to happen via the first law since there is no reservoir at a lower temperature with which the engine can spit out heat. This then implies a violation of KP unless we consider both W and Q to be negative, which reverses the physical picture of what was going on initially - work is now being done on the system and heat is flowing out of the engine into the reservoir.
The conclusion is that an engine taking in heat per cycle must always spit out some heat per cycle to a reservoir if it is to do work. Without this reservoir, it cannot exist.
Is this right? Many thanks.