Derivation of Hydrostatic Equations Fluids

[jdawg]

Homework Statement

I'm having a little trouble understanding how to derive the hydrostatic equations for fluid mechanics!
My professor showed the derivation with respect to y in class, and it kind of made sense to me. Now I'm trying to see if I can derive the equation with respect to z and x.

I think part of my issue is that I don't fully understand the forces that are acting on the fluid particle. I know there are two surface forces and one body force for the y derivation. My professor mentioned that there is only a body force for the y and z directions, but didn't mention x. He said the body force in this case is gravity, which I understand why this force would be on the particle in the z direction, but why the y direction or x direction? How is gravity affecting the particle from the y direction or x direction?

Maybe the body force acting in the y direction isn't gravity? If its not what could it be and why is there no body force in the x direction?

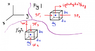
I'm not sure if I drew the forces correctly in the figure 2 for the z direction. I'm also not sure about how to draw the forces for the x direction, would that case just be two surface forces in the x direction? One coming from the front of the box towards the particle and the other coming from the back of the box towards the particle?The summation of forces part I understand no problem. If y'all could help me figure out how to get to that point I think I'll be good!

From picture I attached:
SF1 = (p-(∂p/∂y)(dy/2))dxdz
SF2 = (p+(∂p/∂y)(dy/2))dxdz

SF3 = (p-(∂p/∂z)(dz/2))dxdy
SF4 = (p-(∂p/∂z)(dz/2))dxdy
BodyForceInZ = (ρdxdydz)b_f-z

I hope my picture isn't too confusing, thanks for any help!

 

[Charles Link]

This one is most easily written with one vector equation which you basically have derived above: The force per unit volume from pressure gradients is $f_v=-\nabla P$. The gravitational force per unit volume $f_g=-\delta g \hat{z}$ (using upward as positive z.) In order to have equilibrium the net forces must be zero: $-\nabla P- \delta g \hat{z} =0$. The $-\nabla P$ is in general a vector with 3 components, thereby the x, y, and z equations.

 

[jdawg]

That is much simpler! I think I'm expected to be able to derive each equation for x, y, and z individually though.

 

[Charles Link]

That is much simpler! I think I'm expected to be able to derive each equation for x, y, and z individually though.

$-\nabla P=-[\frac{\partial P}{\partial x}\hat{x}+\frac{\partial P}{\partial y}\hat{y}+\frac{\partial P}{\partial z}\hat{z}]$. The rest is simple. You have one equation for each vector component. The z-component is the only one that has any gravity in it.

 

[Chestermiller]

According to the equations you presented, there is no body force component in the y direction.

 

[jdawg]

Getting the equations isn't the part I'm struggling with, I'm trying to understand what forces are acting on the particle.
I didn't think it made sense for there to be a gravitational force in the x and y directions, but what is the body force if its not gravity?

Sorry I didn't include the body force in the written part, it drew it in the picture attached.

 

[Charles Link]

According to the equations you presented, there is no body force component in the y direction.

Yes, the OP doesn't seem real clear on this. Is their professor considering the possibility of another force, e.g. an electromagnetic force of some kind in the y-direction? Normally, in an introduction to hydrostatics, gravity is the only force to consider besides pressure gradient forces.

 

[jdawg]

There are no electromagnetic forces present, just gravity.

 

[Charles Link]

There are no electromagnetic forces present, just gravity.

Then you normally don't get a body force in the y-direction.

 

[jdawg]

I'm not sure if they'll help, but here's a scan of my notes. Hopefully it isn't so light you can't read them.

 

[Charles Link]

I'm not sure if they'll help, but here's a scan of my notes. Hopefully it isn't so light you can't read them.

I think the professor was talking very loosely. He seemed to be suggesting (from the notes) that you can have a body force in the y-direction, (or any direction for that matter). He didn't say so (at least your notes don't show it), but when other forces besides gravity are introduced in this kind of thing, it is oftentimes some type of electromagnetic force.

 

[jdawg]

Ohh ok, I think that cleared up a lot of confusion. I wish he would've explained that a little better. I was going crazy trying to figure out how gravity was affecting the particle from the y direction. Thanks for y'alls help!

 

[Chestermiller]

Yes, the OP doesn't seem real clear on this. Is their professor considering the possibility of another force, e.g. an electromagnetic force of some kind in the y-direction? Normally, in an introduction to hydrostatics, gravity is the only force to consider besides pressure gradient forces.

I agree. In any event, the professor seems to be allowing for the possibility of a body force other than gravity.