Derivation of Snell's law from Huygens' principle

[moderate]

I am having difficulty accepting an illustration from a physics textbook. The illustration is attached.

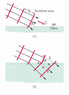
For part (b), the authors state that hec is a right triangle.

Also, the wavefront (cg) is clearly not parallel to the wavefront (he).

However, isn't this impossible?

If point (c) on the wavefront is part of (cg), which is tangential to a circle whose center is point (e), wouldn't (he) necessarily be parallel to (cg) (given that angle (hec) is a right angle) ?

To rephrase my question: how can angle (ecg) not be 90 degrees, given Huygens' principle?

 

[Studiot]

In your diagram look first at the top image.

The red wavefronts are at right angles to three parallel black rays.
The bottom ray has arrived at the glass surface and its continuation arrow is shown refracted. The other two are not. The wave theory basically says that every point on a ray forms a new source. So this point of incidence forms a new source in the glass.

However the waves in the glass formed by this new source have a shorter wavelength.

Now for a wave v = f $$\lambda$$. Since v in glass is less than v in air and since frequency does not alter it follows that

$${\lambda _2} < {\lambda _1}$$

Because of this it follows in your second diagram that

$$\begin{array}{l} hg < ec \\ {\theta _2} < {\theta _1} \\ \end{array}$$

Further in your second diagram the top red wave front is wholely in air and therefore straight, the middle one is partly in air and partly in glass (and thus bent) and the bottom one wholely in glass and straight.

Both triangles hec and hgc are right triangles and they possesses a common hypotenuse, hc.

In answer to one of your questions, remember that gc is wholely in glass so will not be at right angles to ec.


This information should allow you to complete your derivation of Snells Law.

 

[moderate]

In answer to one of your questions, remember that gc is wholely in glass so will not be at right angles to ec.

Hey,

Most of what you are saying makes sense to me.

However, the quoted part is still unclear.

Huygens' principle states that:

Every point on a wave-front may be considered a source of secondary spherical wavelets which spread out in the forward direction at the speed of light. The new wave-front is the tangential surface to all of these secondary wavelets.

Note the word in bold.

The wavelength $$\lambda$$₁ is part of a wavelet that originates at (e).

Since the wavefront (cg) is tangential to this wavelet that originates at (e), and since the wavelet is a circle, the front (cg) must therefore be perpendicular to the radius, (ec).

This is what is causing the confusion.

(note: the wavelet that originates from (e) is not fully a sphere, because the parts of the wavelet that have entered the glass slow down, distorting the spherical shape. however, point (c) is just touching the interface, so it can still be thought of as part of a spherical wavelet)

 

[Studiot]

Since the wavefront (cg) is tangential to this wavelet that originates at (e), and since the wavelet is a circle, the front (cg) must therefore be perpendicular to the radius, (ec).

But none of the 'wavlets' in the glass orignate at e.

Do you understand Huygens principle that you have quoted?

It basically says that everytime the wave reaches a new point (which of course it is doing all the time) that new point can be considered as a new source. The tangential bit applies to new circles emitted from the new point.

So all the way from e to c new points are appearing. As the wave is traveling through the same medium (air) these all 'line up' so the wave travels in a straight line.

As soon as the wave arrives at c and makes c the new centre, the wavelets emitted from c are in the glass and so the wavelength has changed. I don't have time to sketch the circles tonight, but if no one else has done it I will put one up tomorrow.

cg is perpendicular to the radius, but the centre is c not e.

eh is perpendicular to waves circles centred at e

 

[moderate]

Hey,

I think I understand Huygens' principle

Let's consider the wavefront (eh), and call the time when the wave passes through this front t₁.

Then, let's consider the time interval that is equal to $$\frac{\lambda_{1}}{\nu_{1}}$$.

This is equal to the period ($$T$$).

Let us then draw a wavelet that originates at point (e) at t₁.

One point on this wavelet has reached point (c) after time $$T$$. Correct?

The illustration shows the new wavefront (cg), which contains point (c).

This is the point when I disagree with the illustration. Since the line (ec) is a radius of a circle that originates at (e), why isn't $$\angle$$ eCg a right angle?

Is my application of Huygens' principle wrong?

 

[Studiot]

Because g is not on the tangent to the circle with centre e and passing through c and radius ec.

In fact this tangent is not shown in your drawing.

cg is the line tangent to the circle of zero radius, centre c.

 

[moderate]

cg is the line tangent to the circle of zero radius, centre c.

There we go! Now it makes a lot more sense.

I was under the impression that it was a circle of radius (ec) because of the way in which the arc is drawn.

If you look at the illustration, the arc is clearly too large to belong to a circle of zero radius.

I guess the illustrator exaggerated for effect. Or something else along those lines must have happened.

 

[Studiot]

That's Huygen's Principle:

Every new point is a new source. The wave(lets) spread out in circular fashion, the radius starting with zero at the new point and increasing as time goes on.

The rest of the proof is geometry. Are you OK with this?