- #1
E'lir Kramer
- 74
- 0
Spivak, 14.1.iii: Derivative of F, where
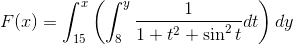
I have the FTC. The answer is also given,
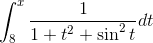
But I don't know how to find it.
First I want to try a function decomposition:
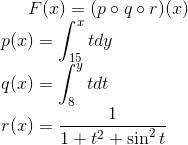
and from the Chain Rule:
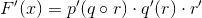 But now I'm stuck. For I do not know an expression for p' or q'. And worse, r' doesn't show up in the given solution. Thanks in advance for your time :).
But now I'm stuck. For I do not know an expression for p' or q'. And worse, r' doesn't show up in the given solution. Thanks in advance for your time :).
I have the FTC. The answer is also given,
But I don't know how to find it.
First I want to try a function decomposition:
and from the Chain Rule: