Derivative of a signal: is it right?

[hastings]

Hi everyone!

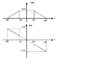
I was trying to solve an old exercise but in a different way. It asks to find the signal x(t) given the graphs of |X(f)| and arg[X(f)]. Please refer to the attachment.

My stategy this time is as follows:
1) find D(f) by deriving |X(f)|
2) antitransform D(f) and get d(t)
3) divide by -j2πt and finally get x(t)

So the first step is finding D(f). From a similarly worked out problem I gathered it should be
$$D(f)= \frac{1}{16} \text{rect}_{4W}(f+4W) - \frac{1}{16} \text{rect}_{4W}(f-4W)$$
However I'm not sure whether the following addend should also be included in D(f):
$$-\frac{1}{4}W \delta(f+2W)+\frac{1}{4}W \delta(f-2W)$$

So ultimately it should be
$$D(f)= \frac{1}{16} \text{rect}_{4W}(f+4W) - \frac{1}{16} \text{rect}_{4W}(f-4W) -\frac{1}{4}W \delta(f+2W)+\frac{1}{4}W \delta(f-2W)$$

Is it right? Or there should be no dirac?
Thank you for your time.

 

[hastings]

Anybody?

 

[Defennder]

I don't think your D(f) is correct. You're not writing it properly, anway. What does the subscript 4w mean for rect? Rect is shifted 4w units to the right and left, and has a scaled width of 4w. How do you write that?

And the sloping line isn't $$f \pm 4w$$. You're supposed to get 0 when you set f=6w but that doesn't give you that.

And I really don't see what's the impulse $$\delta(f \pm 2W)$$ is for. I really don't see any impulses on the graph.

 

[hastings]

What does the subscript 4w mean for rect? Rect is shifted 4w units to the right and left, and has a scaled width of 4w. How do you write that?

When I write $$A\text{rect}_{\Delta}(f-f_0)$$ I mean it's a rect signal with amplitude A (usually a constant), duration Δ and is centered in f_0.
So in this case there are 2 rect signals, one centered in -4W on the left and the other one centered in +4W on the right. Both have a duration of 4W. Here they are, respectively:

$$rect_{4W}(f+4W) \text{ (this is in the negative side)}$$

$$rect_{4W}(f-4W) \text{ (this is on right hand side, positive side)}$$


There is no "A" constant that multiplies the rect signal. There's a slope instead.

And the sloping line isn't $$f \pm 4w$$. You're supposed to get 0 when you set f=6w but that doesn't give you that.

I calculated the 2 slopes in this way:

1) $$\frac{y_1-y_0}{x_1-x_0}= \frac{\frac{1}{4}W -0}{-2W-(-6W)}=\frac{1}{4}W \cdot \frac{1}{4W}=\frac{1}{16}$$ (negative side)

2) $$\frac{y_2-y_3}{x_2-x_3}= \frac{\frac{1}{4}W -0}{2W-6W}=-\frac{1}{16}$$ (for the positive side)


Therefore we have

1)$$\frac{1}{16}f \text{rect}_{4W}(f+4W)$$ this is for the negative side

2) $$-\frac{1}{16}f \text{rect}_{4W}(f-4W)$$ this is for the positive side

The rect acts like a window that catches not the entire slope line but just a piece of it, namely from -6W to -2W for the rising slope (+1/(16) f) and from 2W to 6W for the descending slope (-1/(16) f).

Now, the derivative of a slope is:

$$\frac{d }{df}\bigg[ \pm \frac{1}{16}f \bigg]= \pm \frac{1}{16}$$

i.e. a constant that multiplies the initial rect:

$$D(f)= \frac{1}{16} \text{rect}_{4W}(f+4W) - \frac{1}{16} \text{rect}_{4W}(f-4W)$$


Now let's deal with the $$\delta(f \pm f_0)$$

And I really don't see what's the impulse $$\delta(f \pm 2W)$$ is for. I really don't see any impulses on the graph.

I'm dealing just with |X(f)|, leaving aside Φ(f).
I said I was calculating D(f) which is the derivative of |X(f)| and not |X(f)|, therefore of course you won't find $$\delta(f \pm 2W)$$ on |X(f)|'s graph, it refers to D(f) whose graph isn't given but I need to write its expression somehow.
Again, I'm not sure if $$\delta(f \pm 2W)$$ should appear in D(f) or not. That is exactly my doubt!

 

[Defennder]

I understand your approach now. Earlier I mistakenly thought D(f) referred to |X(f)| itself. If you're differentiating |X(f)| you have to differentiate the rect function itself. You can express the rect function as a function of two Heaviside step functions and then differentiate them to obtain the impulses. So that means you should get 2 delta impulses for each rect, if I'm not mistaken.

The slopes should be shifted as well before differentiating. I couldn't get the same answer as you did using the product rule.

This method seems particularly tedious. Why not start by writing out the original |X(f)| function instead of jumping straight into D(f)? There may be mistakes which are carried forward there.

 

[Redbelly98]

This method seems particularly tedious. Why not start by writing out the original |X(f)| function instead of jumping straight into D(f)? There may be mistakes which are carried forward there.

I agree. Both |X(f)| and Φ(f) are simple linear functions whose equations can be written from inspecting the graphs.