Derivative of e^(x^x) with respect to x

[labinojha]

Homework Statement

Derivative of e^(x^x) with respect to x

Homework Equations

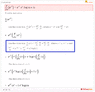
The Attempt at a Solution

Computed using wolframalpha. I have attached the image . Would anyone explain to me the part I have highlighted with the blue box.

 

[BruceW]

imagine that at first, you don't realize that both of the variables are x, so then you have an equation like this: u^v So then, he calculates the total derivative of this equation in a general way, then at the end he replaces u by x and v by x.

Edit: ha, I'm talking about wolfram as a 'he'. Also, there is another way to solve this.

 

[tiny-tim]

hi labinojha!

this is the partial derivative version of the https://www.physicsforums.com/library.php?do=view_item&itemid=353" …

if a depends on b_1,\cdots b_n, and b_1,\cdots b_n depend only on c, then:

\frac{da}{dc}\ =\ \frac{\partial a}{\partial b_1}\frac{db_1}{dc}\ +\ \cdots \frac{\partial a}{\partial b_n}\frac{db_n}{dc}\ =\ (\mathbf{\nabla_b}\,a)\cdot \frac{d\mathbf{b}}{dc}​

in your case, a is x^x, b₁ and b₂ are u and v,

and so a is a function a(u,v) of two variables, and we need to apply the chain rule to each variable separately

(btw, easier would be to say x^x = e^xln(x) )

 

[labinojha]

\frac{\partial}{\partial x}u^{v}=\frac{\partial}{\partial x}u^{v}.\frac{\partial}{\partial x}u+\frac{\partial}{\partial x}u^{v}.\frac{\partial}{\partial x}v

Can i get any reason or possibly a derivation for this ?

Hi tiny-tim!
I had been writing so your answer came before I questioned. :)

http://www.ucl.ac.uk/Mathematics/geomath/level2/pdiff/pd10.html

 

[labinojha]

Hi Bruce!
The other way i used to do it was to take the natural logarithm of both the sides(one side of the equation being y to suppose it as the function) two times in a row and then differentiating them both sides .

Is this what you were talking about ? :)

 

[BruceW]

I was talking about the thing tiny-tim said:
x^x = e^{xln(x)}
But yes, the other way you do it is right as well. I guess there are several equivalent ways to do this problem.