Derive expression for induced voltage and current

[hopkinmn]

Homework Statement

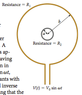
A circular conducting loop with radius a and resistance R2 is concentric with a circular conducting loop with radius b much greater than a and resistance R1. A Resistance dependent voltage is applied to the larger loop, having a slow sinusoidal variation in time given by V(t) = V0 sin ωt, where V0 and ω are constants with dimensions of voltage and inverse time, respectively. Assuming that the magnetic field throughout the inner loop is uniform (constant in space) and equal to the field at the center of the loop, derive expressions for the potential difference induced in the inner loop and the current i through that loop.

Homework Equations

Vind=(d/dt)AB
where A is the area: A=∏a^2
and B is magnetic field

I1=V0/R1
I2=-Vind/R2

The Attempt at a Solution

My understanding is that d/dt=ωcos(ωt)
and B=μ0*I1/(2*∏*b)=μ0*V0/(2*b*∏*R1)

The answer for Vind=-∏*a^2*μ0*V0*ω*cos(ωt)/(2*b*R1)
What I don't understand is what happened to ∏ in B=μ0*V0/(2*b*R1)?

 

[ehild]

My understanding is that d/dt=ωcos(ωt)
and
B=μ0*I1/(2*∏*b)=μ0*V0/(2*b*∏*R1)
The answer for Vind=-∏*a^2*μ0*V0*ω*cos(ωt)/(2*b*R1)
What I don't understand is what happened to ∏ in B=μ0*V0/(2*b*R1)?

Check the formula. There should be no pi in the denominator.

http://hyperphysics.phy-astr.gsu.edu/hbase/magnetic/curloo.html

ehild