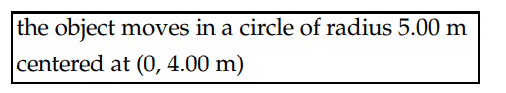SUMMARY
The discussion focuses on the mathematical representation of an object's motion in a circular path within an xy plane, specifically a circle with a radius of 5.00m centered at (0, 4.00m). The equation of a circle, given by (x - x0)² + (y - y0)² = r², is utilized to derive the position functions x = -5sin(ωt) and y - 4 = -5cos(ωt). The participants confirm that substituting these functions into the circle's equation validates the circular motion described.
PREREQUISITES
- Understanding of circular motion and its equations
- Familiarity with trigonometric identities, specifically sin²x + cos²x = 1
- Basic knowledge of parametric equations in physics
- Ability to manipulate algebraic expressions and equations
NEXT STEPS
- Study the derivation of parametric equations for circular motion
- Learn about the applications of trigonometric identities in physics
- Explore the concept of angular frequency (ω) in circular motion
- Investigate the relationship between circular motion and harmonic motion
USEFUL FOR
Students and educators in physics or mathematics, particularly those focusing on circular motion and trigonometric applications in kinematics.