Detecting gradual change in an oscillating data set.

[woodssnoop]

Hello:

I have been trying to find some information on choosing the width of a running average over a time dependent data set. Here is an example of what I am dealing with:

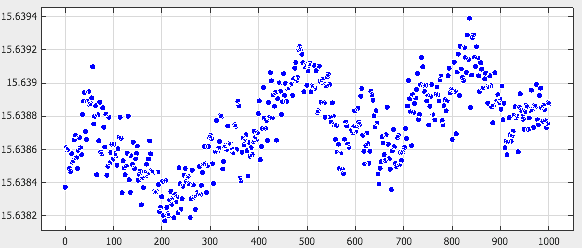
The oscillations should be around the line y=15.6385 and I am wondering if there is a way to quantitatively detect gradual change in a oscillating system. If I do a linear fit of this data I get a line with a positive slope so I get the feeling that there is a gradual change.

Any help would be nice. Thank you.

 

[Stephen Tashi]

To get a mathematical answer to a problem there must be enough "givens" and what constitutes an answer ("detect" in this particular case) must be precisely defined.

In real world problems, it's usually necessary to make many assumptions before there are enough "givens". Most people don't want to bother with this and they also don't want to say exactly what they expect of an answer.

If you don't want to formulate a precise mathematical problem, then I'd say the positive slope of your regression line already is a kind of "detection" of gradual increase.

If you want to use traditional (i.e. frequentist) statistics, you can assume the regresson line is the flat one. Then you must assume some probability model for how the errors are generated. If you do that, you end up with a quantification of the probability of observing data similar to what you have. Based on the that answer, you can make your own subjective decision about whether the regression line is really flat. This would define "detecting".

You can pick a more complicated model for how the data is generated (such as an ARIMA model). GIven the visual impression that your data has waves in it, that kind of model seems more approriate than a linear model. I think you could also quantify the probability of getting similar data if you assume such a model.

If you take a Bayesian statistical approach you consider a entire collection of probability models and assign a probability distribution that gives the "a priori" probability for each of them being the one that nature chose. Then you compute the "posterior" probability distribution which tells you the probability each model was chosen given the data you observed. If you have to pick a particular model as "the" answer, this is still a subjective decision. It does seem natural to pick the one that is most likely if the posterior distribution has a peak.