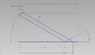
rajeshmarndi said:
From the picture i.e attached. Can there be a formula, where the ball will strike after certain number of hit, say on side b, what will be the angle the ball will make after n successive hit.
I think it is just not possible, one can only measure the next angle the ball will make, provided one know the present position where the ball has hit.
Thank you.
There are formulas for everything you want, given the initial position, direction, and the dimensions of the rectangle.
To make things simpler, instead of having a grid that is WxH in size, set up a matrix where every cell is the size of the rectangle.
Now, instead on bouncing, the ball simply crosses from one cell to another. If it starts by moving to the left, the first time it crosses a vertical line it will correspond to side B and then it will switch back and forth between B and D. Similarly for moving right, up, and down. Every time is crosses a horizontal line, the cell will correspond to a mirror image of the previous cell - switched top-to-bottom. For a vertical line - switch left to right.
Since the B-side vs D-side switches every other time, and crossing a vertical line causes the polarity to switch every other time, crossing vertical lines will not cause the angle at B to change. On the other hand, every time it crosses a horizontal line, the angle will switch.
So let's say that the ball starts along the bottom of the HxW rectangle from a point that is X from the bottom left corner where 0<=X<=1 and 0 is the left corner and Y is the right corner. Then, it strikes the left side at a point that is Y from the bottom left corner where 0<=Y<=1. So, on the first bounce, it will strike side B at an angle of S=atan(HY/WX). On subsequent bounces it will strike at either +S or -S.
On the Nth bounce, it will have traveled horizontally W(2(N-1)+X) and vertically H(Y/X)(2(N-1)+X). The number of horizontal lines it would have crossed would be that vertical distance divided by the height and truncated to an integer: Int((Y/X)(2(N-1)+X)).
Since the angle will flip that number of times, we will take modulo 2 and generate the sign of the angle from that:
atan(HY/WX) (1-2(Mod2(Int((Y/X)(2(N-1)+X)))))