Homework Help Overview
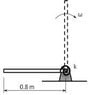
The problem involves determining the angular velocity of a bar released from a horizontal position and passing through a vertical position, utilizing the principles of dynamics and conservation of energy. The context includes a torsional spring and gravitational potential energy considerations.
Discussion Character
- Exploratory, Conceptual clarification, Mathematical reasoning, Assumption checking
Approaches and Questions Raised
- Participants discuss the application of conservation of energy, identifying types of energy involved, including elastic potential energy and gravitational potential energy. There are attempts to clarify the correct expressions for these energies and their roles in the problem.
Discussion Status
Participants are actively engaging with the problem, questioning assumptions about energy calculations and the behavior of the center of mass. Some guidance has been offered regarding the setup of energy equations and the importance of measuring height changes correctly.
Contextual Notes
There is ongoing confusion regarding the calculation of gravitational potential energy and the height of the center of mass as the bar transitions from horizontal to vertical. Participants are also discussing the moment of inertia relevant to the problem.