Determine the change in elevation of mercury in this manometer

[Bolter]

Homework Statement

See below

Relevant Equations

pressure = rho x g x h

Having some trouble in answering this question

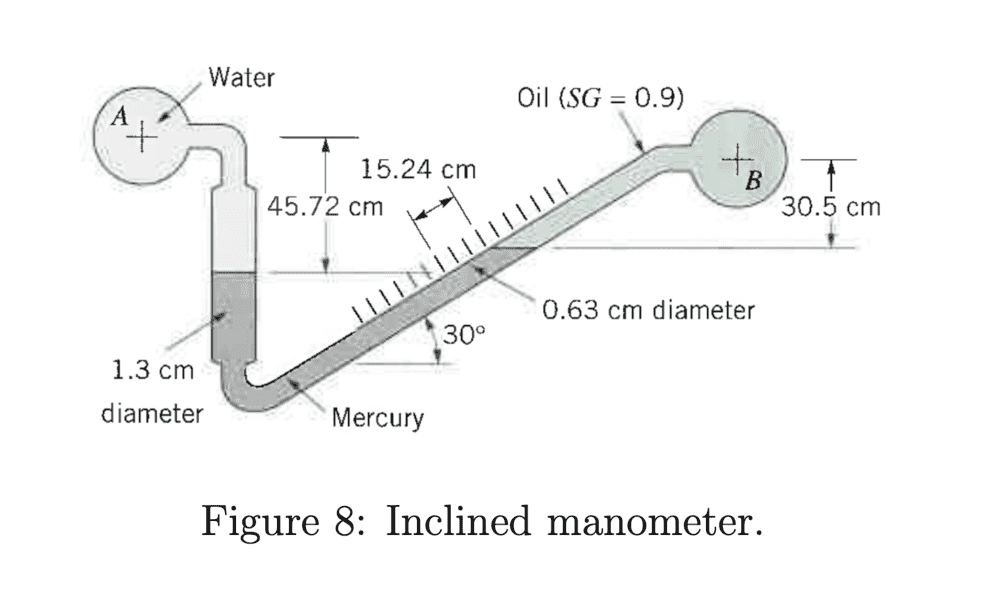
What I have done so far is calculate the initial pressure difference, then used that to find the new pressure difference when pipe's A pressure increases by 34.4 kPa

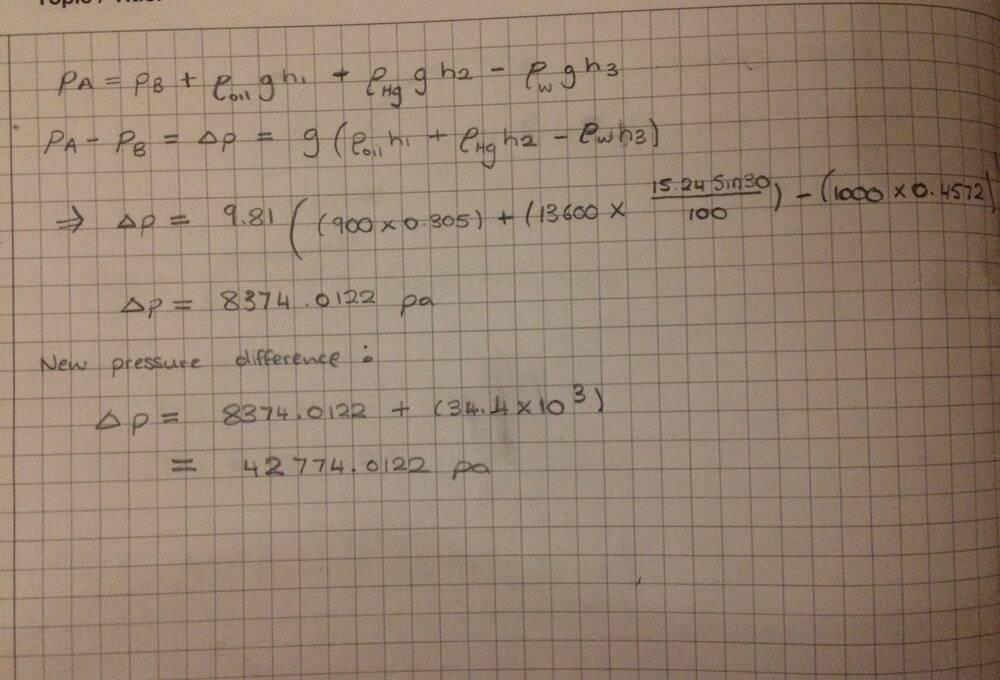
Not too sure of where to carry on from here? All I know is that if pipe A is exerting a bigger pressure then the mercury level on the left arm would decrease. But I can't seem to figure by how much this decrease would be

I would be grateful for any help. Thanks!

 

[haruspex]

Go back to your equations where h1, h2, h3 are variables. As the pressure increases, all three will change, but in a related way. What is the relationship between the changes?

 

[Bolter]

Go back to your equations where h1, h2, h3 are variables. As the pressure increases, all three will change, but in a related way. What is the relationship between the changes?

Well of course depth of water column (h3) would increase by x
and mercury column (h2) would also increase but by y
and oil column (h1) would decrease by y

I can’t seem to express the changes of h1,h2 and h3 in terms of x or y only
as I’m dealing with left arm and right arm having 2 different radii

 

[haruspex]

Well of course depth of water column (h3) would increase by x
and mercury column (h2) would also increase but by y
and oil column (h1) would decrease by y

I can’t seem to express the changes of h1,h2 and h3 in terms of x or y only
as I’m dealing with left arm and right arm having 2 different radii

Think about the volume of the mercury.

 

[Bolter]

Think about the volume of the mercury.

Is it that the volume of mercury that gets displaced in the left arm is equal to the same volume of mercury that gets pushed up in the right arm?

 

[haruspex]

Is it that the volume of mercury that gets displaced in the left arm is equal to the same volume of mercury that gets pushed up in the right arm?

Well, the total volume of mercury is not going to change, is it?

 

[Bolter]

Well, the total volume of mercury is not going to change, is it?

No it wouldn't. This is what I have done

I let x be the thing we're trying to find i.e. the change in depth of mercury in left arm

Therefore can I say:
water column depth increases to 0.4572 + x
oil column depth decreases to 0.305 - (4.2579x *sin30)

And the difference in height of mercury columns must increase to 0.0762 + x + (4.2579x *sin30)

Is this alright?

 

[haruspex]

No it wouldn't. This is what I have done

View attachment 270317

I let x be the thing we're trying to find i.e. the change in depth of mercury in left arm

Therefore can I say:
water column depth increases to 0.4572 + x
oil column depth decreases to 0.305 - (4.2579x *sin30)

And the difference in height of mercury columns must increase to 0.0762 + x + (4.2579x *sin30)

Is this alright?

I don't know how you get the 0.0762m, but it doesn’t matter; what matters is the change in the differential height of the mercury arms.

 

[Bolter]

I don't know how you get the 0.0762m, but it doesn’t matter; what matters is the change in the differential height of the mercury arms.

0.0762m was the initial depth of mercury column from doing 15.24cm * sin30 = 0.0762m

 

[haruspex]

0.0762m was the initial depth of mercury column from doing 15.24cm * sin30 = 0.0762m

Ok

 

[Bolter]

Ok

Thanks so now taking all those as my new variables (all in terms of x) in replacement of h1,h2 and h3, I get the following

I'm sure I done the math right but I got the new change in elevation of mercury to be 0.077m whereas the correct answer is actually 0.083m? Not entirely sure what I did wrong

 

[haruspex]

Thanks so now taking all those as my new variables (all in terms of x) in replacement of h1,h2 and h3, I get the following

View attachment 270319

I'm sure I done the math right but I got the new change in elevation of mercury to be 0.077m whereas the correct answer is actually 0.083m? Not entirely sure what I did wrong

You seem to be confused over the meaning of $\Delta P$. The information given is the change in pressure at A, but your calculations look like you are treating it as the difference in pressure between A and B.
As I noted, the given 15.24 cm is irrelevant; likewise the 30.5cm and 45.72cm.
Anyway, I got 8.85cm.

 

[Bolter]

You seem to be confused over the meaning of $\Delta P$. The information given is the change in pressure at A, but your calculations look like you are treating it as the difference in pressure between A and B.
As I noted, the given 15.24 cm is irrelevant; likewise the 30.5cm and 45.72cm.
Anyway, I got 8.85cm.

But wait I realized I did make a mistake in my workings in post #11 as I should've written -1000(0.4572 + x) on my third line and not -1000x

so now I got an answer of 0.088m or 8.8cm. I could of got 8.85cm if I rounded to more decimal places

I'm sorry but I don't understand though, why would 15.24cm, 30.5cm and 45.72cm be irrelevant if I used them in my calculations to help me get to an answer of 8.8cm

 

[haruspex]

But wait I realized I did make a mistake in my workings in post #11 as I should've written -1000(0.4572 + x) on my third line and not -1000x

View attachment 270323
so now I got an answer of 0.088m or 8.8cm. I could of got 8.85cm if I rounded to more decimal places

I'm sorry but I don't understand though, why would 15.24cm, 30.5cm and 45.72cm be irrelevant if I used them in my calculations to help me get to an answer of 8.8cm

Ok, I see now what you did. In your first post you calculated a ΔP as the initial difference in pressure between A and B, then in post #11 you calculated a new 'ΔP' in terms of x. I misinterpreted that as the change in pressure at A.
But you can see that the whole of your original ΔP canceled out, so you did not need to have calculated it. You could just have used
$34.4kPa=gx(\rho_{Hg}-\rho_w+\frac 12\frac{D^2}{d^2}(\rho_{Hg}-\rho_{oil}))$.

 

[Bolter]

Ok, I see now what you did. In your first post you calculated a ΔP as the initial difference in pressure between A and B, then in post #11 you calculated a new 'ΔP' in terms of x. I misinterpreted that as the change in pressure at A.
But you can see that the whole of your original ΔP canceled out, so you did not need to have calculated it. You could just have used
$34.4kPa=gx(\rho_{Hg}-\rho_w+\frac 12\frac{D^2}{d^2}(\rho_{Hg}-\rho_{oil}))$.

I would have never been able to make such a concise expression for the change in pressure from the one you have shown above, but I believe I could have stuck to only the change in pressure at A and done this. Which still gives me the same answer as before

 

[Bolter]

Ok, I see now what you did. In your first post you calculated a ΔP as the initial difference in pressure between A and B, then in post #11 you calculated a new 'ΔP' in terms of x. I misinterpreted that as the change in pressure at A.
But you can see that the whole of your original ΔP canceled out, so you did not need to have calculated it. You could just have used
$34.4kPa=gx(\rho_{Hg}-\rho_w+\frac 12\frac{D^2}{d^2}(\rho_{Hg}-\rho_{oil}))$.

Also if the answer is 0.0885m is the answer in the textbook wrong? They gave 0.083m instead

 

[Chestermiller]

I get 0.089 m

 

[Bolter]

I get 0.089 m

Yeah 0.089 m and 0.088 m (from rounding 0.0884656m) are close enough, there is probably a minimal difference caused due to using slightly rounded values in the prior calculations