Determining Force applied so mass will stay at rest

AI Thread Summary
To keep a mass of 12.5 kg at rest, a force must counteract its weight, calculated as 122.5 N using the formula W = mg. Participants suggest drawing a free body diagram of the pulley above the mass to analyze the forces involved. The tension in the rope must equal the weight of the mass for it to remain stationary. Understanding the equilibrium of forces acting on the pulley is crucial to solving the problem. Proper analysis will reveal the necessary force to maintain the mass at rest.
uazaga
Messages
11
Reaction score
0
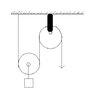
A weight of mass 12.5 Kg hangs from very light pulleys as shown in fig. What force must be applied to the rope so that the mass stays at rest.

M=12.5 Kg
W=mg
a=g=9/8 m/s^2

M=12.5 Kg
W = mg = 12.5 x 9.8 = 122.5 N
I've done this much but I have no clue what to do now. Can someone please help me out?
 

Attachments

  • Untitled.jpg
    Untitled.jpg
    7.6 KB · Views: 427
Last edited:
Physics news on Phys.org
the figure doesn't show, therefore i am unable to help u, if u want u can send it to my email so i can try it. its [email address deleted by moderator]
 
Last edited by a moderator:
Can you find the tension in each part of the rope and relate it to the weight you have calculated? Hint: Draw a free body diagram of the pulley that is directly over the hanging mass. If that pulley is at rest, what must be true about the forces acting on it?
 
Last edited:

Thread 'Errors and significant figures'

I multiplied the values first without the error limit. Got 19.38. rounded it off to 2 significant figures since the given data has 2 significant figures. So = 19. For error I used the above formula. It comes out about 1.48. Now my question is. Should I write the answer as 19±1.5 (rounding 1.48 to 2 significant figures) OR should I write it as 19±1. So in short, should the error have same number of significant figures as the mean value or should it have the same number of decimal places as...
View full post »
Thread 'A cylinder connected to a hanging mass'

Thread 'A cylinder connected to a hanging mass'

Let's declare that for the cylinder, mass = M = 10 kg Radius = R = 4 m For the wall and the floor, Friction coeff = ##\mu## = 0.5 For the hanging mass, mass = m = 11 kg First, we divide the force according to their respective plane (x and y thing, correct me if I'm wrong) and according to which, cylinder or the hanging mass, they're working on. Force on the hanging mass $$mg - T = ma$$ Force(Cylinder) on y $$N_f + f_w - Mg = 0$$ Force(Cylinder) on x $$T + f_f - N_w = Ma$$ There's also...
View full post »

Similar threads

Distribution of Energy when work is done on a system of 2 masses connected by a spring
Replies
17
Views
1K
Calculating acceleration of a prism and block connected to a wall through a rope and pulley
Replies
4
Views
330
Finding the Force Applied by a Support on a Falling Chain
Replies
2
Views
2K
Newton's law problem: Pushing 2 stacked blocks on a horizontal table
Replies
13
Views
3K
Calculating Applied Force for a Moving Block on a Table
Replies
9
Views
4K
Calculating Net Force of 3 Blocks in an Elevator
Replies
9
Views
2K
Force applied on the pulley of a system
Replies
8
Views
3K
Find the force to push a book sideways on a table
Replies
2
Views
2K
Balancing a Seesaw: Finding Mass with Torque
Replies
7
Views
10K
What is the energy conservation principle in a two masses and pulley problem?
Replies
33
Views
4K

Hot Threads

Recent Insights

Back
Top