jskillz411
- 2
- 0
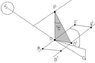
so imagine you have an airplane traveling at an axis projecting a signal vertically down along AF axis and you have some point O on AF axis and a refference angle Sun-O-Plane . the plane gets affected by some rolling motion at a certain known angle... now the axis shifts to A'F' and O become O' I drew a little picture to show my idea. I'm trying to come up wit a correction formula to find out what the new Sun-O'-Plane angle would be .The sun could be at any position. and the information known would be the S-o-P angle along with the planes altitude.
any feed backs guys would be great =)
any feed backs guys would be great =)