MHB Diagonal Crossing Challenge: 800x200 Rectangle

[mathmaniac1]

Challenge:
How many boxes are crossed by a diagonal of an 800 X 200 rectangle?

Solution with proof required...

 

[caffeinemachine]

Challenge:
How many boxes are crossed by a diagonal of an 800 X 200 rectangle?

Solution with proof required...

Hello Mathmaniac
I don't understand the question. What us meant by 'boxes are crossed'.

Also, if this is a challenge problem then shouldn't this go in the 'Challenge and Puzzles' forum?

 

[MarkFL]

Yes, I sent the OP a VM asking if this is a challenge or if it is a problem for which he needs help shortly after it was posted, but have not gotten a response yet. Once the matter is settled, I will move it if need be, then remove this post so that the topic is not cluttered.

 

[mathmaniac1]

Challenge:

Its a challenge,Mark...

 

[mathmaniac1]

I don't understand the question. What us meant by 'boxes are crossed'.

Here is an example:

View attachment 709

The boxes inside the rectangle are meant to be squares...

 

[MarkFL]

Its a challenge,Mark...

I have thus moved the topic to the Challenge Questions and Puzzles sub-forum. I know you used the word "Challenge" but wanted to make sure it fit the criteria, i.e., you have the correct solution ready to post in the event no one solves it.(Wink)

 

[mathmaniac1]

Yes!

 

[Nono713]

Spoiler

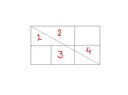
The rectangle is made of $800 \times 200$ "boxes". The diagonal thus has gradient $\pm \frac{200}{800} = \pm \frac{1}{4}$, where a "box" has unit dimensions. Note the diagonal starts at the top left corner of the top-left-most box. This is important. So, after 4 units of width travelled, the diagonal will intersect the top left corner of another box:​

And this section of the diagonal intersects four boxes. Since the rectangle is 800 boxes wide, this section of the diagonal will repeat $\frac{800}{4} = 200$ times, and so the diagonal intersects $4 \times 200 = 800$ boxes.​

---

A more interesting problem is to consider a rectangle of dimensions $p \times q$ where $p$ and $q$ are distinct primes. Then the diagonal never intersects the top-left corner of a box within the rectangle, and a different approach is called for:​

 

[mathmaniac1]

Thats right,Bacterius...
And can you show your approach for distinct primes?

 

[Nono713]

Thats right,Bacterius...
And can you show your approach for distinct primes?

Spoiler

It's simple enough, in fact. Because we know that the diagonal will, in this case, never intersect a corner, we can count the number of boxes crossed by simply counting the number of times the diagonal intersects both the vertical sides and the horizontal sides of the boxes. The diagonal will intersect $p - 1$ horizontal sides, and $q - 1$ vertical sides, simply by virtue of being a line crossing the rectangle from top-left to bottom-right (or top-right to bottom-left).

But not so fast - the diagonal always starts inside the rectangle, and so automatically intersects the top-left box (or whichever corner of the rectangle you start your diagonal from), which we haven't yet considered, giving a total of $(p - 1) + (q - 1) + 1 = p + q - 1$ boxes intersected. Checking with the diagram above gives $11 = 7 + 5 - 1$ boxes intersected, as expected.

Not very rigorous, just a proof sketch showing the general approach.​

 

[mathmaniac1]

Here we have a winner!