Tonik
- 13
- 0
I took a placement test and blew it away. (I tested into calculus, best possible placement for this test.) Everything was rather simple except for this problem which I cannot seem to get right. Can someone show me where I'm going wrong here?
Use x2+2 in the Difference Quotient.
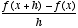
(x+h)2+2-(x2+2)
x2+xh+h2+2-x2-2
[STRIKE]x2[/STRIKE]+xh+h2[STRIKE]+2[/STRIKE][STRIKE]-x2[/STRIKE][STRIKE]-2[/STRIKE]
(xh+h2)/h
(x[STRIKE]h[/STRIKE]+h[STRIKE]2[/STRIKE])/[STRIKE]h[/STRIKE]
x+h
This answer was not a given choice. Any ideas where I'm messing up?
(I'm sure I making stupid mistake somewhere that I'm overlooking)
Homework Statement
Use x2+2 in the Difference Quotient.
Homework Equations
The Attempt at a Solution
(x+h)2+2-(x2+2)
x2+xh+h2+2-x2-2
[STRIKE]x2[/STRIKE]+xh+h2[STRIKE]+2[/STRIKE][STRIKE]-x2[/STRIKE][STRIKE]-2[/STRIKE]
(xh+h2)/h
(x[STRIKE]h[/STRIKE]+h[STRIKE]2[/STRIKE])/[STRIKE]h[/STRIKE]
x+h
This answer was not a given choice. Any ideas where I'm messing up?
(I'm sure I making stupid mistake somewhere that I'm overlooking)