A Differential Equation to Difference Equation

[ebangosh]

Hi all,

I am a bit new in this, am trying to learn DE, dynamical systems, & chaos. I am looking into some answers for the following questions:

1) Is it always possible to derive a difference equation for every differential equation, and if so how do we do that?

2) Consider Lorenz system:

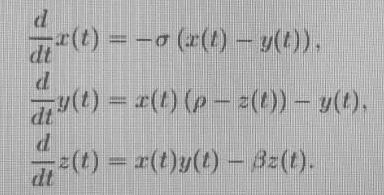
Where does Lorenz map/discrete version coming from, was it derived from Lorenz system?

3) I heard about Baker's map but I couldn't figure if Baker's map was also derived from a system of linear differential equation too?

4) If the original system of differential eqns exhibits chaotic characteristic, will this characteristic remains in difference equation?

Thanks for your helps.

 

[hilbert2]

It's possible to form many kinds of difference equations from any DE or PDE. Some of them are better, some worse. The goal is to find a difference equation that is not numerically unstable, i.e. doesn't produce a solution where the numerical error accumulates exponentially with increasing $t$.

Any characteristic of the original DE, including chaos, should remain in the discrete solution if the numerical scheme is any good. Actually, the small numerical errors in a discretized solution can often initiate chaos even if the initial conditions are carefully set to produce an (unstable) periodic trajectory.

 

[ebangosh]

Thank you for your answers. I am trying to absorb them. When you mention 'some of them are better, some worse', did you mean numerically stable and unstable respectively?

How do we test whether the difference equation still own the chaotic characteristics?

If we are modelling real world phenomena, initially using DE/PDE, then after we transform into difference equation, is the model still valid? Is there any sort of threshold on any parameter telling such a thing?

Thank you.

 

[hilbert2]

The methods differ in both stability and in how short finite difference $\Delta t$ has to be used in the place of $dt$ to get reasonable accuracy. Try to google some info about Euler and "leapfrog" finite difference methods as an example.

Chaos is tested by doing several calculations with slightly different initial conditions.

The finite difference integration should reproduce the most important features of the original differential equation. For instance, when integrating the time dependent Schrödinger equation, the norm of the wave function should remain constant (unitary time evolution).