Mistake Not...
- 2
- 0
Hi there,
I was reading up on Holonomic constraints and came across this equation on the Wikipedia page:
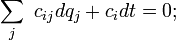
The page says it is a differential form. Can anyone explain the notation for me or provide a link or two to documents or pages which explain this notation?
Thank you very much,
Geoff
I was reading up on Holonomic constraints and came across this equation on the Wikipedia page:
The page says it is a differential form. Can anyone explain the notation for me or provide a link or two to documents or pages which explain this notation?
Thank you very much,
Geoff