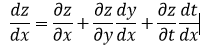I Difficulty with function dependencies f(u,x)

[D O]

If you have a function x = x(u,t)
then does u necessarily depend on x and t? so u = (x,t)
For example, if x(u,t)=u^2 t it seems that because t=x/u^2, t=t(x,u)

I am having difficulty working out the general equation for dz \over dx if z=z(x,y,t) x=x(u,t)y=y(u,v,t)
The chain rule suggests it should be:

But I don't know how to simplify dy \over dx or dt \over dx, as neither y nor t depends on x directly or indirectly.

I can easily work out dz \over dt because t is at the bottom of the tree of dependency, but x is not.

Can you have cyclic dependencies? Or are all dependencies cyclic? What does this mean for the chain rule?
Thanks.

 

[PeroK]

If you have a function x = x(u,t)
then does u necessarily depend on x and t? so u = (x,t)
For example, if x(u,t)=u^2 t it seems that because t=x/u^2, t=t(x,u)

I am having difficulty working out the general equation for dz \over dx if z=z(x,y,t) x=x(u,t)y=y(u,v,t)
The chain rule suggests it should be:

But I don't know how to simplify dy \over dx or dt \over dx, as neither y nor t depends on x directly or indirectly.

I can easily work out dz \over dt because t is at the bottom of the tree of dependency, but x is not.

Can you have cyclic dependencies? Or are all dependencies cyclic? What does this mean for the chain rule?
Thanks.

You can look at $z$ either as a function of $x, y, t$ or a function of $u, v, t$. In either case, you can't have a total derivative $\frac{dz}{dx}$. If $u, v$ were also functions of $t$, you could calculate $\frac{dz}{dt}$.

 

[D O]

Thanks for the answer!
So does that mean you can only calculate a total derivative wrt x when ALL the dependencies of z eventually depend on x?
You can look at z as a function of (x,y,t) or of (u,v,t); I assume this mens you could also look at it as a function of (x,u,v,t) by substituting for y.

How do you know which way to look at z when solving a problem?
Can x be seen as a function of z or is the dependency one-way and linear?

 

[Stephen Tashi]

If you have a function x = x(u,t)
then does u necessarily depend on x and t? so u = (x,t)

You appear to be asking whether u is a function of (x,t) rather than the more general use of the word "depends".

For example, if x(u,t)=u^2 t it seems that because t=x/u^2, t=t(x,u)

The example relevant to your initial question is u^2 = x/t , which is satisfied by both u = \sqrt{x/t} and u = - \sqrt{x/t}, so u is not a function of (x,t). However u "depends" on (x,t) in the sense that when you are given (x,t) you can't pick the value of u arbitrarily. Your choices are somewhat restricted.

I am having difficulty working out the general equation for dz \over dx if z=z(x,y,t) x=x(u,t)y=y(u,v,t)
The chain rule suggests it should be:

The "general equation" can't be worked out, because, in general, if you have a function z = f(x,y,t) then the notation \frac{dz}{dx} and the concept "the derivative of z with respect to x" isn't necessarily meaningful unless z happens to be a function of x alone - either explicitly or implicitly. The chain rule itself doesn't guarantee the existence of \frac{dz}{dx}.A slightly more general question is whether:
eq. 1) \frac{\partial z}{\partial x} = \frac{\partial z}{\partial x} + \frac{\partial z}{y} \frac{\partial y}{\partial x} + \frac{\partial z}{t} \frac{\partial t}{\partial x}

That's a tricky question ! Does " \frac{\partial z}{\partial x}" denote the same thing on the left hand side of eq. 1 as it denotes on the right side of that equation ?

We can distinguish two different meanings for " \frac{\partial z}{\partial x}" . These are:

1. The partial derivative of z(x,y,t) with respect to the variable x
and
2. The partial derivative of z(x,y,t) with respect to the value of its first argument.

For example if z(x,y,t) = x^2 + yt and y = x^3 (and t is independent of x ) then "the partial derivative of z with respect to its first argument) is 2x where "x" denotes the value of the first argument, but the "partial derivative of z with respect to the variable x" is 2x + 3x^2 t, where "x" denotes the value of the variable x.

Some books use the subscript notation z_x(x,y,t) to denote interpretation 1) and the notation like z_1(x,y,t) to denote interpretation 2.

The dx, dy style notation is convenient for many purposes, but it obscures the fact that functions are evaluated at particular arguments. For example, the chain rule can be denoted as (F(g(x)))' = F'(g(x)) g'(x) which makes it clear than F' must be evaluated at the argument g(x) rather than the argument x.

I'll write more about this topic, but right now I have to leave to meet someone at a hardware store.

 

[PeroK]

Thanks for the answer!
So does that mean you can only calculate a total derivative wrt [/itex]xwhen ALL the dependencies of z eventually depend on x?<br /> You can look at z as a function of (x,y,t) or of (u,v,t); I assume this mens you could also look at it as a function of (x,u,v,t) by substituting for y.<br /> <br /> How do you know which way to look at z when solving a problem?<br /> Can x be seen as a function of z or is the dependency one-way and linear?

<br /> <br /> A total derivative applies when all variables depend on a single parameter. The most obvious example is time. If you have a function of the spatial coordinates $x, y, z$ (e.g. the gravitational potential), then those spatial coordinates are independent and that function has partial derivatives with respect to each spatial coordinate.<br /> <br /> Let&#039;s call than function $V(x, y, z)$.<br /> <br /> Now, if you have a particle with a defined trajectory - often parameterised by time - then you have a new function of that single parameter, which we can call $f$:<br /> <br /> $f(t) = V(x(t), y(t), z(t))$<br /> <br /> This gives us the potential at each point of the particle&#039;s trajectory.<br /> <br /> Where $(x(t), y(t), z(t))$ is the particle&#039;s trajectory. Note that $x(t), y(t), z(t)$ are no longer independent variables. And now you can apply the chain rule to get the derivative $\frac{df}{dt}$.<br /> <br /> But, if $x, y, z$ are functions of two variables - $u, v$ say - which might define a surface, then we can define:<br /> <br /> $g(u, v) = V(x(u, v), y(u, v), z(u,v))$<br /> <br /> And his gives us the potential at each point on the surface. Note here that we have partial derivatives (not total derivatives) of $g$ wrt $u, v$.

 

[D O]

Thanks for both your answers, they are very helpful.
I am interested about the different meanings of \partial z \over \partial x.
I can see applications for z_x (such as finding the minima/maxima of a 2d function), but when would you use z_1?
It seems that if you want to calculate z_x you can't just ignore what y is a function of, as I would have done if I had been calculating it (and would have instead calculated z_1.

 

[D O]

The example relevant to your initial question is u2=x/t u^2 = x/t , which is satisfied by both u=√x/t u = \sqrt{x/t} and u=−√x/t u = - \sqrt{x/t} , so u u is not a function of (x,t) (x,t) .

This was a bad example, as there are two solutions for u.
Would u be a function of (x,t) if instead x=x(u,t)=u+t?
Then you could argue that u=x-t so u depends on x and t.
Do you have to specify which variables are independent and which are dependent?

 

[Stephen Tashi]

It seems that if you want to calculate z_x you can't just ignore what y is a function of, as I would have done if I had been calculating it (and would have instead calculated z_1.

Yes, you are correct that if you wish to compute the interpretation of \frac{\partial z}{\partial x} in the sense of z_x, you must consider all the arguments of the function z that depend on x.

In the example, you can get the correct answer from the chain rule by using

$z_x = z_1 \frac{\partial x}{\partial x} + z_2 \frac{\partial y}{\partial x} + z_3 \frac{\partial t}{\partial x}$

using

$z_1 = 2x ,\ z_2 = t,\ z_3= y$
$\frac{\partial x}{\partial x} =1,\ \frac{\partial y}{\partial x} = 3x^2 ,\ \frac{\partial t}{\partial x} = 0$

How and whether such a formal manipulation makes sense is something I'd have to think about!

From the point of pure mathematics, the notation used in applied mathematics is truly horrifying in its ambiguity. In pure mathematics, a "function" involves two sets, a domain D and a co-domain C. The function is a set of ordered pairs of elements $F$ consisting of ordered pairs $(d,c)$ such that $d \in D$ and $\ c \in C$ and no two distinct ordered pairs in $F$ have the same first member.

Two functions are different functions if they have different domains or different co-domains or one contains an ordered pair that the other doesn't.

Take that pure mathematical view and try to reconcile it with a typical applied math scenario like:

Let $z(x,y,t) = x^2 + yt$ and let $y = x^3$

How many functions are involved in this scenario ? - and which function does "$z$" denote ?

First we have the function $z$ whose ordered pairs are of the form $( (x,y,t), x^2 + yt )$. The first member of the ordered pair is a triple of real numbers and the second member of the ordered pair is a real number. For example, this function $z$ contains ( (1,2,3),7 ).

If we incorporate the "side condition" $y = x^3$ into our concept of $z$ we have $z = x^2 + x^3 t$, which consists of ordered pairs of the form $(x,t), x^2 + x^3t)$ where the first member of the ordered pair is an ordered pair of real numbers $(x,t)$ instead of an ordered triple of real numbers. This second concept of $z$ as function does not contain ((1,2,3),7).

Since $z$ is ambiguous as notation for a function, the notation $\frac{\partial z}{\partial x}$ is also ambiguous. The distinction between $z_1$ and $z_x$ isn't because "there are two different partial derivatives for the same function". The distinction arises because there are two different functions that are denoted by the same symbol "z".
In the example. $z_1$ denotes a partial derivative of a function $z$ whose ordered pairs are of the form $((x,y,t) x^2 + yt)$ and $z_x$ denotes a partial derivative of a function $z$ whose ordered pairs are of the form $((x,t), x^2 + x^3t)$.

In addition to the ambiguous notation for functions, we have the complication of the term "variable". It is so difficult to define the notion of "variable" precisely that pure mathematics only does it in contexts like the study of formal languages. In typical math courses (applied or pure) we don't find a clear definition of concept of a "variable" that is on par with other precise definitions - such as the definition of a function or the definition of a derivative etc. If an instructor says "I'll list the variables on the upper left corner of the marker board" we assume "variables" is a term from common speech on par with the terms "upper left corner of the marker board". Both "variable" and "upper left corner of the marker board" can be explained in colloquial language, but the course proceeds without giving either concept a precise mathematical definition.

In the above example, we can ask tricky questions like "Is $y$ a variable? Is $y$ a function? Is $y$ both a function and a variable?.

Those questions don't have specific answers unless we establish a specific context. To use the term "variable" unambiguously, we should being by speaking of a specific function. For example, if the ordered pairs of a function F are of the form ((x,y,t),z then "the variable y" is just away of referring to "the second element of the first member of an ordered pair of F. But if we are considering the function " $y = x^3 t$" then $y$ is a way of referring to the function itself and also to the second member of an ordered pair of the form $((x,t), x^3t)$.

When you have several statements involving the symbol "$y$" you have the problem of deciding whether the "$y$" in one statement has the same meaning as the "$y$" in another statement. In applied math, we learn to cope with such ambiguities.

In applications a "variable" usually represents something like "temperature" that is not a mathematical abstraction. In a context such as "temperature z is a function of x,y,t" then "z"can be used to refer to a function or a "dependent variable" In a context such as "pressure p is function of temperature z", the symbol "z" can refer to a "independent variable".

Would u be a function of (x,t) if instead x=x(u,t)=u+t?
Then you could argue that u=x-t so u depends on x and t.

Yes, if the relation x = u + t holds among 3 variables then we use ambiguous notation and use "u" to denote both the variable u and also the function defined by ordered pairs ( (x,t) x-t). However this does not mean that the concept of u as a function is identical to the concept of u as a variable.

Do you have to specify which variables are independent and which are dependent?

When you state precisely what function you are considering then this shows which symbols represent dependent and independent variables. The same symbol may be used to denote the dependent variable in one function and an independent variable in a different function.