A Dipole moment operator and perterbations

[Paintjunkie]

TL;DR Summary

regarding the way the dipole moment operator is handled in perturbation theory. electric and magnetic cases

I am reading a PHD thesis online "A controlled quantum system of individual neutral atom" by Stefan Kuhr. In it on pg46, he has a Hamiltonian

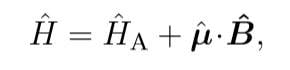
I am also reading a book by L. Allen "optical resonance and two level atoms" in it on page 34 he starts with a Hamiltonian where the perturbation is the same with the E operator instead of B.

They both develop this in the same manner saying that the dipole operator can be represented as

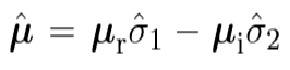
They both use the Heisenberg picture and eventually arrive at the following (Allen has E operator instead of B)

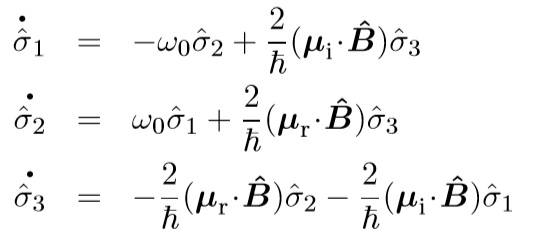
So I guess my question is. how come this is ok? Am I to assume the general treatment is fine, but when it comes down to actually calculating the dipole matrix elements they would be different? In my Jackson E&M book, on page 296, I see that E and B would have the same form, they are not really operators there though... I am just a little confused.

I myself as trying to use a Bloch Sphere to represent the interactions of resonant microwaves and an off resonant laser on a two level system. So I am thinking to develop it the same way the two of them do. I believe that it was Feynman, Vernon, and Hellwarth that developed this, but I have not actually looked at their derivation.

 

[Paintjunkie]

To add to this, my confusion comes when the Bloch Sphere is finally derived from it. It seemed like the pseudospin vectors that were derived in both cases were the same, and that led to the same Bloch vector. But if I expose my system to an on resonance magnetic pulse from t0 to t1 and then at an electric pulse from t1 to t2. am I moving around the same sphere?

 

[vanhees71]

Well, the two sources obviously treat different physical situations. I don't have Allen's book at hand, but I guess he considers the usual (non-relativistic?) treatment of the semiclassical theory of an atom, i.e., the interaction of an atom (with the electrons described by non-relativistic QT) with an external classical electromagnetic field in the dipole approximation, i.e., the interaction with this external field is, in dipole approximation, given by $\hat{H}_{\text{int}}=-\hat{\vec{d}} \cdot \vec{E}.$
The interaction with the magnetic field is neglected (it's part of the next order of the multipole expansion).

The PhD thesis, publicly available online here:

http://hss.ulb.uni-bonn.de/2003/0191/0191.htm

deals with an atom in a magneto-optical trap, and there the author treats the motion of the atom in the magnetic field. I'm only a bit puzzled about the sign in Eq. (4.1). I don't know why he write $\hat{H}_{\text{int}}=+ \hat{\vec{\mu}} \cdot \vec{B}$ instead of having a - sign on the right-hand side.

 

[Paintjunkie]

good eye, seems to be a typo to me, quick look in QM Griffiths tells me it should be minus.

The MOT should not matter, I don't think... the magnetic coils for the MOT should be turned off when the microwaves are perturbing the atom. In my lab, we use an anti-Helmholtz config (I think all MOT's do? The thesis seems to say he does.) so you can approximate B=0 at the middle anyways.

The end result is unchanged, the equations that the Pauli operators follow is the "same" in both cases(with E swapped for B) ill include a picture of Allen.

I was really under the impression that in the thesis the microwaves were the ones perturbing the system (bottom of page 45). Because of what happens immediately after on page 46, I thought that the microwaves were imparting a electromagnetic wave whose contribution was mostly magnetic.

A quick look in QM Griffiths (pg348) seems to contradict this. saying that an atom interacting with a passing light wave responds mainly to the electric part.

I think it has something to do with a symmetry argument. something about the hyperfine states having spherical symmetry and so the electric dipole moment is zero. but I don't really get that.