Direction of Axle Force on Pivoted Disk

[LovePhys]

Hello everyone,

I came across this problem from my Physics textbook.

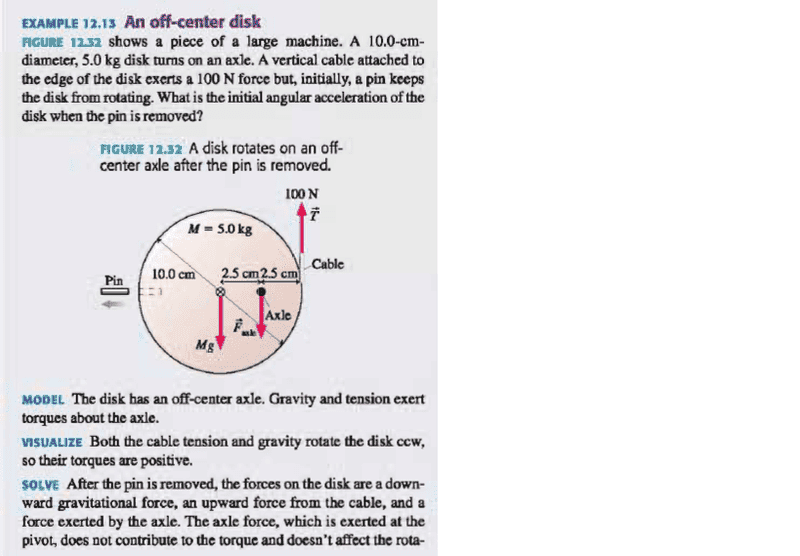
I do not understand why the direction of the axle force is pointing downward. I think the upper part of the disk is exerting a downward force on the pivot (as it is pulled down by the Earth's gravity), and according to Newton's third law, the pivot should exert an upward force on the upper part of the disk?

Please correct if I am wrong, thank you very much!
LovePhys

 

[tiny-tim]

Hello LovePhys!

I do not understand why the direction of the axle force is pointing downward. I think the upper part of the disk is exerting a downward force on the pivot (as it is pulled down by the Earth's gravity), and according to Newton's third law, the pivot should exert an upward force on the upper part of the disk?

The weight is about 50 N down, and the cable force is about 100 N up,

so the force from the axle has to be about 50 N down.

 

[LovePhys]

@tiny-tim:
Thank you for your reply.

I think I know what you mean. Do we generally identify the direction of all the forces and leave the axle force to the last?
Oh, and can you please have a look at this problem for me? It is the same kind of question. I don't understand why they say: "Because the plank is resting on the supports, not held down, forces n1 and n2 must point upward. The supports could pull down if the plank were nailed to them..."

Thank you very much indeed!
LovePhys

 

[tiny-tim]

Hi LovePhys!

(just got up :zzz:)

Do we generally identify the direction of all the forces and leave the axle force to the last?

Yes, that's exactly correct.

The axle force is a single reaction force, ie an unknown force, and so (in equilibrium) it must be equal and opposite to the resultant (the vector sum) of all the known forces.

(you're probably more familiar with the reaction force on body A from body B being equal and opposite to the reaction force on body B from body A, but it's also equal and opposite to all the other forces on body A, in equilibrium )

btw, it's the same with eg the normal force for an object being pulled along a slope … we find all the known forces, and then the normal force is calculated to balance them

(and also for the kinetic friction force for steady motion … kinetic friction is also an unknown force, since all we know is it's less than µN)

in 2D you can have 2 reaction forces, and find them this way (using moments), and in 3D you can have 3 reaction forces, and find them this way …

if you have more than 2 (or 3) reaction forces, the problem is indeterminate, and you can only solve it with extra information, about the bending properties of the object

… I don't understand why they say: "Because the plank is resting on the supports, not held down, forces n1 and n2 must point upward. The supports could pull down if the plank were nailed to them..."

They mean
i] as shown, the planks are not nailed, therefore the supports can't pull them down, therefore the reaction force must be either up or zero
ii] if the planks are nailed, then obviously the reaction force could be up zero or down

So if you add all the known forces, and the resultant is down, then in both cases the reaction force is up.

But if you add all the known forces, and the resultant is up, then in the second case the reaction force is down, but in the first case equilibrium is impossible and the plank will rise.

 

[LovePhys]

@tiny-tim:

Thank you, you have been so helpful. Btw, sorry for the late reply, I've been thinking about what you said to make sure that I do understand them! But still, I have a problem with this:

it's the same with eg the normal force for an object being pulled along a slope … we find all the known forces, and then the normal force is calculated to balance them

(and also for the kinetic friction force for steady motion … kinetic friction is also an unknown force, since all we know is it's less than µN)

in 2D you can have 2 reaction forces, and find them this way (using moments), and in 3D you can have 3 reaction forces, and find them this way …

if you have more than 2 (or 3) reaction forces, the problem is indeterminate, and you can only solve it with extra information, about the bending properties of the object

In Newtonian mechanics, I've never thought that the normal force could be an unknown force. Normally, I have a block moving up an incline or something like that, then the block is not in equilibrium as it's moving, and also I admit that I just draw the direction of the normal force intuitively based on the hint that it is "normal" to the contact surface.

 

[tiny-tim]

Hi LovePhys!

(just got up :zzz:)

But still, I have a problem with this:
…
In Newtonian mechanics, I've never thought that the normal force could be an unknown force. Normally, I have a block moving up an incline or something like that, then the block is not in equilibrium as it's moving, and also I admit that I just draw the direction of the normal force intuitively based on the hint that it is "normal" to the contact surface.

I'm not sure what your question is.

as to direction, the general term is "reaction force"

("normal" is simply another word for "perpendicular", from the latin word "norma" meaning a mason's set-square)

sometimes it is obvious that the reaction force is normal to the surface

but usually even the direction is unknown

in that case, we usually arbitrarily resolve the reaction force into two perpendicular components, which we call the normal force and the friction force …

but those two forces aren't really separate forces at all, and we only pretend they are for convenience

 

[LovePhys]

@tiny-tim: Your post has answered my question! I have learned something new, thanks a lot!