Disk rolling down a hill with no sliping

[dislect]

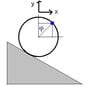
A disk with mass m and radius R is rolling down a hill with no slipping, until it reaches a wall and then stops:

I want to write a set of equations describing the position cordinates x and y of the disk's center of mass (point A) and the cordinates for point B.

mgsin(theta)=ma -> gsin(theta)=a -> gsin(theta)=dv/dt ; V_B=2wR ; V_A=wR

Can you help me figure this out and guide me towards the solution?

Thanks,
Sharon

 

[ehild]

The CM moves as if the whole mass was centred there, under the effect of all forces acting on the disk.
You wrote the component of gravity along the slope as force, but there is an other one, which makes the disk rolling instead of slipping. What is it?

You can also use conservation of energy to find out the velocity of the CM and angular velocity of the rotation of the disk.

If you have figured out the motion of the CM, the point on the rim performs circular motion around the CM, with angular velocity v_CM/R. You have to add the velocities ; those of translation and rotation.

ehild

 

[dislect]

You mean friction?
Is it correct to say that my coefficient of friction is mew=1, giving me:
mgsin(theta) - mgcos(theta) = ma ?

using energy:
mg(h+R)=0.5mv^2

I still wonder how i am using these equations to create the connection between cordinates x,y of points A and B to time,mass,radius,height,angle ?

 

[dislect]

Ignore my last message,

1. -f+mgsinθ=mx'' , 2. N=mgcosθ Forces equations
3. -fR=-0.5mR^2 * θ'' Momentum equation
4. Rα''=-x'' Pure rolling condition

After some algebra i get:

5.1 x''=2/3 gsinθ
5.2 α''=-2/3 * g/R * sinθ
5.3 f=1/3 mgsinθ
5.4 N=mgcosθ

And as long as μ>1/3 tanθ there is a pure roll with no slip

x'=2/3 gtsinθ+x'(0)=2/3 gtsinθ , x(t)=1/3 gt^2 sinθ+x(0)=1/3 gt^2 sinθ

Now, how do I find x(t) and y(t) for points A and B ?

 

[ehild]

You mean friction?
Is it correct to say that my coefficient of friction is mew=1, giving me:
mgsin(theta) - mgcos(theta) = ma ?

using energy:
mg(h+R)=0.5mv^2

It is static friction (Fs) between the disk and slope that does not let the disk slip. Static friction is not a force of defined magnitude: it has got the necessary magnitude. The static friction decelerates the translation of the CM, but accelerates rotation.

You have two equations, one between forces and acceleration of CM:

ma=mgsinθ-Fs

the other for torque (FsR), moment of inertia (I) and angular acceleration dω/dt

Idω/dt=R Fs,

You have the condition of rolling Rω=V_CM, which holds also for the accelerations Rdω/dt=a.
Eliminate Fs and you get the acceleration a.

ehild

 

[dislect]

I posted another message, can you take a look at the equations I wrotre there?

 

[ehild]

And as long as μ>1/3 tanθ there is a pure roll with no slip

x'=2/3 gtsinθ+x'(0)=2/3 gtsinθ , x(t)=1/3 gt^2 sinθ+x(0)=1/3 gt^2 sinθ

Now, how do I find x(t) and y(t) for points A and B ?

You have found x(t): it is the position of point A along the slope, till the disk is on the slope. It is not the x coordinate so it would be better to use s(t) instead of x(t). x(t)=s(t)cos(theta)
You get the change of y as the y coordinate of the displacement, and add the initial height: yi=h+R

For x>L1, the disks moves on the horizontal track with constant velocity.

As for the point on the rim, write up its position in terms of the position of the CM and the position of B with respect to the CM.

ehild

 

[dislect]

I got another question, this dosent add up but it seems like the mass plays no role in the motion. is that correct?

 

[ehild]

I got another question, this dosent add up but it seems like the mass plays no role in the motion. is that correct?

It does not matter.

ehild

 

[dislect]

thanks you, you had been a great up!
now I am left with writing the x(t) equation for the center of mass while moving on the plane (x>L1), how do i approach this one?
is it correct to say that now my x(t)=sqrt(2gH)*t + x(0)=sqrt(2g*(h+R)) + 0 ?

 

[ehild]

The disk will roll further with the same speed and angular speed as it reached the bottom of the slope, and the change of height is h. The CM can not go deeper than the radius. The initial potential energy transforms to the sum of KE of the translation and KE of rotation.

ehild

 

[dislect]

the equations i wrote don't work for me could you tell me where i went wrong?
what i did was
mgh=0.5mv^2
v=x'=sqrt(2gh)
x=sqrt(2gh)t+x(0)=sqrt(2gh)t+L1

 

[ehild]

the equations i wrote don't work for me could you tell me where i went wrong?
what i did was
mgh=0.5mv^2
v=x'=sqrt(2gh)
x=sqrt(2gh)t+x(0)=sqrt(2gh)t+L1

That is not true.

mgh is equal to the total kinetic energy: 1/2 mv²+1/2 Iω².


ehild

 

[dislect]

Thanks,
now i know that I=0.5mR^2, i know R,m and h
though I am not sure how do i find the ω ? is it v/R ?

 

[ehild]

Thanks,
now i know that I=0.5mR^2, i know R,m and h
though I am not sure how do i find the ω ? is it v/R ?

In case of pure rolling, it is.

ehild