Do Wedge Constraint Relations Affect Velocities Parallel to the Contact Surface?

[newbie12321]

TL;DR Summary

Why is there no constraint on the component of velocities parallel to the contact surface?

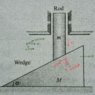
There’s a rigid rod pushing on a wedge. Velocity of the rod is v, which is vertically downwards, and the wedge is sliding to the right as a result with a velocity u. There is zero friction on the surface of the wedge and the surface of the rod in contact with the wedge.
According to wedge constraint relations, if the rod stays in contact with the wedge, then its relative velocity with respect to the wedge perpendicular to the contact surface must be zero. It means velocity of the rod and the wedge perpendicular to the contact surface must be equal, i.e

vcosθ = usinθ

My question is, what about their velocities parallel to the contact surface? Is there no constraint on their velocities parallel to the contact surface if both the rod and the wedge have to stay in contact?

If their relative velocity parallel to the contact surface is non-zero, the rod will keep sliding down the wedge, won’t it lose contact with the wedge after it reaches the bottom? Likewise, if the rod were sliding up the wedge, won’t it lose contact when it finally comes off the top of the wedge? Hope I am able to explain what I want to understand. Is it because the wedge doesn’t extend infinitely? This is something I am not able to understand. Please help me with it. I have attached a picture. Thanks

*Edit : Angle of inclination of the wedge is θ, not α

 

[A.T.]

Is it because the wedge doesn’t extend infinitely?

That's not a velocity constraint, but a displacement constraint.

 

[newbie12321]

That's not a velocity constraint, but a displacement constraint.

My question is, is there no constraints on their velocities parallel to the contact surface?

 

[A.T.]

My question is, is there no constraints on their velocities parallel to the contact surface?

Why would there be any?

 

[BvU]

If you require contact with the wedge, there is only ONE constraint .

You can express it in many ways, all equivalent (e.g. the one you mention).

 

[newbie12321]

Why would there be any?

Like I have said in my post, if the component of relative velocity between the rod and the wedge parallel to the contact surface is non-zero, the rod will slide off the edge and will lose contact with the wedge as a result. That's what got me wondering as to why there is no constraint on their velocities parallel to the contact surface?
Hope I am able to explain it well

 

[newbie12321]

If you require contact with the wedge, there is only ONE constraint .

You can express it in many ways, all equivalent (e.g. the one you mention).

If you require contact with the wedge, there is only ONE constraint .

You can express it in many ways, all equivalent (e.g. the one you mention).

If the component of relative velocity between the rod and the wedge parallel to the contact surface is non-zero, would the rod not slide off the edge of the wedge, and lose contact with it as a result?

 

[A.T.]

Like I have said in my post, if the component of relative velocity between the rod and the wedge parallel to the contact surface is non-zero, the rod will slide off the edge and will lose contact with the wedge as a result. T

Like I have said in my post, the size of the ramp imposes a displacement constraint, not a velocity constraint.

 

[newbie12321]

Like I have said in my post, the size of the ramp imposes a displacement constraint, not a velocity constraint.

Got it. Thanks a lot.