Does Distance Contraction Cause Time Dilation?

[morrobay]

Its my understanding that relativistic length contraction l = l₀√ 1-v² also applies to the
space itself in the moving S' system. For example a rocket traveling at .6 c.
A distance that is 1000 meters in S frame is contracted to 800 meters in rockets frame. (1000/γ)
Therefore the elapsed time / proper time in rocket S' frame ( 800m/.6c) is less than
as calculated as seen from stationary S frame ( 1000m/.6c.)
Hence time dilation equated to length/distance contraction.
And allowing the proper"time between ticks" of both clocks, S and S' being equal.

 

[Ibix]

You are correct that the distance between two points (e.g. marker bouys at relative rest) varies between frames in the same way regardless of whether they are connected or not. I'd be reluctant to call that "space contracting" because what's actually happened is that you've changed your mind about what you mean by "space".

There are three basic effects between frames in special relativity - length contraction, time dilation, and the relativity of simultaneity. Arguably, the relativity of simultaneity is the most fundamental, since that is more or less directly a statement that the two frames are using different coordinate systems. But I would say that neither of length contraction and time dilation is logically prior to the other - neither causes the other. It's kind of like asking whether the vertical side causes the horizontal side to be shorter than the hypotenuse in a right triangle, or vice versa. Neither, really. It's just the way (Minkowski) geometry works.

 

[morrobay]

Would Δt' = γ(Δt - vΔx) the elapsed time in S' frame agree numerically with 800m/.6c ?
And Δt = γ( Δt' +vΔx') the elapsed time in S frame agree numerically with 1000m/.6c ?

 

[Dale]

Arguably, the relativity of simultaneity is the most fundamental

And even if it is not most fundamental, it is definitely the most challenging concept for students to internalize. That makes it the source of most of the "paradoxes" in SR.

 

[Ibix]

Would Δt' = γ(Δt - vΔx) the elapsed time in S' frame agree numerically with 800m/.6c ?
And Δt = γ( Δt' +vΔx') the elapsed time in S frame agree numerically with 1000m/.6c ?

Yes, by definition of velocity. Note that in the rocket's rest frame, the destination comes to the rocket and not vice versa. Also note that you can phrase it either way round - $\Delta t=\Delta x/v$ has the same content as $\Delta x=v\Delta t$. But the choice of simultaneity criterion is usually the choice you make that leads to the Lorentz transforms. That was the point I was making above.

 

[nitsuj]

Its my understanding that relativistic length contraction l = l₀√ 1-v² also applies to the
space itself in the moving S' system. For example a rocket traveling at .6 c.
A distance that is 1000 meters in S frame is contracted to 800 meters in rockets frame. (1000/γ)
Therefore the elapsed time / proper time in rocket S' frame ( 800m/.6c) is less than
as calculated as seen from stationary S frame ( 1000m/.6c.)
Hence time dilation equated to length/distance contraction.
And allowing the proper"time between ticks" of both clocks, S and S' being equal.

In turn c is still invariant...seemingly the source of this difference in measures of length / time (speed = length/time)

 

[morrobay]

Would Δt' = γ(Δt - vΔx) the elapsed time in S' frame agree numerically with 800m/.6c ?
And Δt = γ( Δt' +vΔx') the elapsed time in S frame agree numerically with 1000m/.6c ?

I have a follow up question pertaining to the start and stops process of the stationary clocks. I do not think the relativity of simultaneity applies.
Event 1 is when the rocket passes the origin moving in x direction. at .6c t = t' = 0 . x = x' = 0.
A light flash from rocket to stationary clock in z direction starts both S and S' clocks.
Event 2 is when rocket passes marker at x =1000 m and a light flash stops the second stationary clock adjacent to x = 1000 m marker in z direction as well as the clock in S' rocket.
If this experimental setup is correct then again as above, Δt' ∠ Δt

 

[Ibix]

Yes, from the invariant interval. In S, $\Delta t$ and $\Delta x$ are non zero. In S', $\Delta t'$ is non zero but $\Delta x'$ is zero. The interval between the two events must be the same calculated in either frame, so $c^2\Delta t'^2=c^2\Delta t^2-\Delta x^2$, which implies $\Delta t'<\Delta t$.

 

[Meir Achuz]

Does Distance Contraction Cause Time Dilation?
Neither one causes the other. Each can be derived from Lorentz transformation, so either one could be derived from the other by working backward and then forward.

[Moderator's note: edited to remove bold and pick a reasonable font size.]

 

[morrobay]

Does Distance Contraction Cause Time Dilation?
Neither one causes the other. Each can be derived from Lorentz transformation, so either one could be derived from the other by working backward and then forward.

[Moderator's note: edited to remove bold and pick a reasonable font size.]

Understood ! But what I am intending to show follows: When Δx' = 0
Δt = γ Δt' and
Δτ = γ Δt' so
Δt = Δ τ and
Δt' = Δτ/γ = Δτ' Then while elapsed time in S' is less than elapsed time in S , (Δt' = Δt/γ)
And was also pointed out by Ibix : c² Δt'² = c²Δt² - Δx²
the "time between ticks" in S' clock = S clock

By the way. The start time for S, clock at x = 1000m (in post #7) pre advanced by d/c is from light flash from S, x = 0 t = 0

 

[Ibix]

@morrobay - as requested, I had a re-read of this. I'm rather confused by your experimental design. Where do you have clocks? You refer to clocks in S and S' being started and stopped by flashes of light. Where exactly are these clocks? One on the rocket and one each at the start and end markers of the course? Where is the light flash emitted from? The rocket, or one or other of the course markers?

I initially interpreted your setup as having one clock on the ship and one on each marker, the latter two synchronised in the Einstein sense. Then you measure the transit time in S using the difference in clock readings on the two marker clocks when the rocket passes, and in S' using the elapsed time on the rocket clock. But now I think you are using light flashes in a more complex way, and their travel time may need to be factored in.

Also, in #10 you have started referring to proper time. Proper time is often called "wristwatch time", because it is the elapsed time on your personal timekeeping device. But that means you need to say that whose wristwatch you are talking about and the time between what events on their worldline. Since you specified only two events and everything is inertial there can be only one proper time between them.

I'm not saying your conclusions are wrong, just that you need to set out your experiment with more care so that we can follow what you are trying to do. Perhaps a diagram?

 

[morrobay]

(1) Rocket , v = .6c left of origin, (vt₁ )² = (ct₁)² - (ct₂)² sends light flash to mirror in S. Rocket clock starts at x = x' = 0.
Reflected light travels to clock in S at x = 1000m marker. This clock pre. advanced . by d/c starts.
(2) Light flash from rocket left of x = 1000m by (vt₁)² stops clock in S frame as it passes 1000m marker when rocket clock is also stopped.

The elapsed time in rocket clock Δt' = Δτ' is 800m/.6c
The elapsed time in S frame is Δt = Δτ = 1000m/.6c

 

[Ibix]

I think I understand what you are trying to do now. You are trying to measure the rocket's travel time in S using a single clock and without having to worry about the relativity of simultaneity. Right? If not, I still haven't understood what you are trying to do

If so, it's impossible. If it were possible then there would be an absolute sense of simultaneity and you'd break relativity. On a more concrete note, why did you choose to advance your second clock by d/c? The answer is because you assumed that the one-way speed of light was the same in both directions, which is equivalent to adopting Einstein's synchronisation convention.

The time you call Δτ is the proper time of the second clock at rest in S between an event on its worldline simultaneous (in Einstein's sense) with the rocket passing the first clock and the event of the rocket passing the second clock.

 

[morrobay]

Yes I was measuring travel time in S,Δt ,with one clock located at x = 1000m. Light flash from rocket strikes mirror when rocket passes origin .( see diagram) light then starts clock with photo cell at x = 1000m in S frame. Since that signal is not instantaneous the clock at 1000m must be advanced by 1000m/.6c in order to measure travel time from t₀ to t₁ when rocket passes x = 1000m marker
You have said this is not possible. So then how would observers in S start and stop the clocks in accord with simultaneity that would be in agreement with calculated travel times :
Δt = 1000m/.6c = 5.5 ⋅ 10^-6 s
Δt' = γ ( Δt - vΔx/c²)
Δt' = 6.94 ⋅ 10^-6 s - 2⋅10^-6 s = 4.94⋅10^-6 s
Edit: Δt' = 6.94 ⋅ 10^-6 s - 2.5⋅10^-6 s = 4.44⋅10^-6 s
That is apprx Δt/λ , .8 ( 5.55⋅10^-6s) = 4.44⋅10^-6 and also
= 800m/1.8 ⋅ 10⁸ m/sec
Then Δt' also equals Δτ'

 

[Ibix]

You misunderstand me. Your methodology works fine. But it is not independent of the relativity of simultaneity, which is what you seem to be claiming in #7. That comes into it through your choice to pre-advance your clock by d/c, which is equivalent to starting it at zero at the same time as the light pulse leaves the start marker (i.e. simultaneously in the Einstein sense).

So your methodology measures the coordinate time in S between the events "rocket passes the start marker" and "rocket passes the end marker". This is also the proper time of the clock between the events on its worldline "simultaneous with the rocket passing the start marker" and "rocket passes the end marker". But since the starting event is chosen using some simultaneity criterion, that proper time doesn't have any particular significance.

I'm on my phone at the moment. I'll try to draw a diagram later.

 

[Ibix]

As promised, a diagram restating my last post. I've slightly simplified your experimental setup. There are two markers, the "start" marker painted red and the "end" marker painted blue. The rocket is painted purple and passes arbitrarily close to the two markers. In this way I can get rid of your mirror - the red marker is touching the rocket when the light pulse is emitted, so it is received with zero travel time, and the pulse goes direct to the blue marker. This is plotted on the Minkowski diagram below. I've also added the path of the light pulse in yellow.

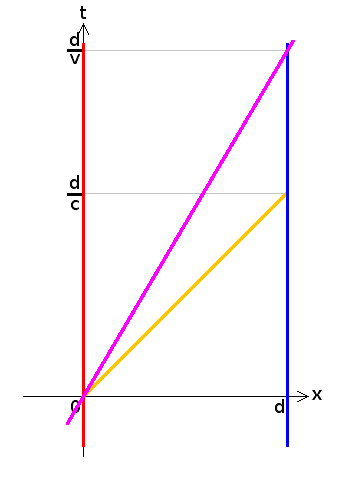
Basically a Minkowski diagram is a displacement-time graph, with the time axis up the page and with units where the speed of light is one (e.g. seconds for time and light seconds for distance). I've drawn this one in the rest frame of the markers, so their worldlines (blue and red) are vertical (their x coordinate is not changing with coordinate time). Both the rocket (purple worldline) and the light pulse (yellow worldline) are moving to the right, so their worldlines slope right (their x coordinate is increasing with coordinate time). The wordline of the light pulse has a slope of 1 because it is traveling at c - one light second per second. The worldline of the rocket has a slope of 1/0.6 because it is traveling at 0.6c (I only sketched it - don't yell at me if the gradient's wrong).

The rocket passes the red marker at time zero and emits a light pulse which starts the clock at the blue marker when it gets there (when the yellow line crosses the blue line). The rocket stops the clock when it reaches the blue marker (when the purple line crosses the blue line). So what your clock actually measures is the interval along the blue line between where the yellow line and purple lines cross it. Since the start and stop events are defined by observable physical things, any observer can measure space and time coordinates of each event and calculate the interval between and must come up with the same answer. However, you pre-set your blue clock to d/c. In other words you added the interval between the events "blue line crosses the x axis" and "yellow line meets blue line". But there's nothing special about the first of those two event. There's no way for any observer to spot "blue worldline crosses x axis" because the x-axis is just something I drew on the diagram. And I could have chosen a different simultaneity convention, which would really just be a matter of rotating the x axis. It changes nothing about the worldlines, but renders your choice of d/c meaningless.

The particular choice of simultaneity criterion that I've made (or, Einstein made and I copied) is a very sensible one. But it is a choice, not a physical necessity.