eyeweyew
- 35
- 6
- TL;DR
- Does path independence still hold if permittivity is non-uniform
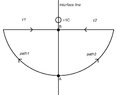
Consider a scenario in the picture where one half of space consists of a material with permittivity ϵ1 and the other half consists of a material with permittivity ϵ2, where ϵ1 > ϵ2. A unit positive charge is fixed at the interface between the two materials. Path1 is entirely within the material with permittivity ϵ1 and Path2 is entirely within the material with permittivity ϵ2. The paths are reflectively symmetric, with the interface acting as the mirror line. Just for simplicity, also assume the arc part of the both paths is perpendicular to the electric field comes from the fixed charge so they don't contribute to the work. Does it still require the same amount of work to move a unit positive charge from point A to point B along Path1 and Path2?
$$W=\int_{A}^{B}\overrightarrow{E}\cdot\overrightarrow{dl}$$
where $$\overrightarrow{E} = \frac{1}{4\pi\epsilon r^2}\widehat{r}$$
Attachments
Last edited: