Does the Center of Mass Have Horizontal Velocity in a Frictionless System?

[cacofolius]

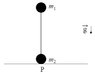
Hi. There are two masses connected by a massless bar, and from the unstable equilibrium position shown in the figure is slightly inclined so it falls down, being the final state of the system that both masses are in contact with the surface. There is no friction between the floor and m₂. The problem is to find the horizontal component of the velocity of the center of mass.

I think that since there is no friction, and gravity being the only outside force that acts on the system, the center of mass will fall straight down, so there will be no horizontal velocity of it. So is this right?

$$Vx = \frac{m_{1}V_{x1}+m_{2}V_{x2}}{m_{1}+m_{2}} = 0$$

Thanks in advance.

 

[cacofolius]

I thought I was on Homework, please excuse me. I'm looking for how to move/delete the thread. Edit: I just found out I can't. All apologies.

 

[Dale]

No problem, I moved it for you. Usually we require the use of a template, but you essentially provided the key elements of the template anyway. So it should be OK.

Your analysis seems correct to me.

 

[cacofolius]

Thank you very much!

 

[HalfLostAndSearching]

Hello,

Based on the information provided, your approach seems correct. Since there is no friction and gravity is the only external force acting on the system, the center of mass will fall straight down without any horizontal velocity. This means that the horizontal component of the center of mass velocity will be equal to zero.

The equation you provided, Vx = (m1Vx1 + m2Vx2) / (m1 + m2) = 0, is the correct expression for calculating the horizontal component of the center of mass velocity. This is known as the center of mass formula, and it is used to calculate the overall motion of a system of masses.

In this case, since the system is in an unstable equilibrium position, it will fall down due to the force of gravity. As the masses fall, they will eventually come into contact with the surface, and at this point, the center of mass will have a zero horizontal velocity, as you correctly stated.

I hope this helps to clarify your understanding of the problem. Keep up the good work!