nonequilibrium
- 1,412
- 2
Apologies for the atrocious attempt at a drawing:
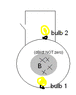
So my professor said that if you close the switch, the upper lightbulb (n° 2) will go out. How exactly do you know this? Well of course, if you replace the changing magnetic field that is inducing an emf with a battery somewhere close to lightbulb 1, it is evident the 2nd bulb will go out once you close the switch, and that you can argue with 1/R = 1/R_a + 1/R_b. But this doesn't seem to be a valid argument in this case, does it? Because I could say "imagine the (B-field replacing) battery is not close to the first bulb, but rather close to 2, on that little piece between the bulb and the rectangular connection, in which case the other bulb would stop burning if you closed the switch."
I suppose I would've found it most logical if all the bulbs kept burning once you closed the switch, but apparently this is not the case. How would one argue light bulb 2 goes out?
Thank you,
mr. vodka
EDIT: Is maybe the following reasoning a correct way to do this: (R_1: first bulb; R_2: second)
Close the switch. Go around the circular loop: I_1 R_1 + I_2 R_2 = emf
Go around the loop containing the switch and bulb 1: I_1 R_1 = emf
=> I_2 = 0
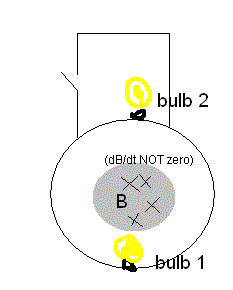
So my professor said that if you close the switch, the upper lightbulb (n° 2) will go out. How exactly do you know this? Well of course, if you replace the changing magnetic field that is inducing an emf with a battery somewhere close to lightbulb 1, it is evident the 2nd bulb will go out once you close the switch, and that you can argue with 1/R = 1/R_a + 1/R_b. But this doesn't seem to be a valid argument in this case, does it? Because I could say "imagine the (B-field replacing) battery is not close to the first bulb, but rather close to 2, on that little piece between the bulb and the rectangular connection, in which case the other bulb would stop burning if you closed the switch."
I suppose I would've found it most logical if all the bulbs kept burning once you closed the switch, but apparently this is not the case. How would one argue light bulb 2 goes out?
Thank you,
mr. vodka
EDIT: Is maybe the following reasoning a correct way to do this: (R_1: first bulb; R_2: second)
Close the switch. Go around the circular loop: I_1 R_1 + I_2 R_2 = emf
Go around the loop containing the switch and bulb 1: I_1 R_1 = emf
=> I_2 = 0