Does this equation have a name?

[gamow99]

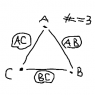
I'm trying to figure out how many times my computer will have to loop through an array. I'm building a logic calculator so it's checking contradictions. If there are four sentences, a b c d, then one has to check the following combinations to see if there is a contradiction

ab
ac
ad
bc
bd
cd

The equation seems to be, let n = the number of sentences:

(n - 1) + (n - 2) + (n - 3)

But that's not a good equation because it does not inform us how many things to add together.

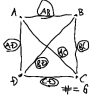
If there are six sentences then the equation would be

(n - 1) + (n - 2) + (n - 3) + (n - 4) + (n - 5)

There has to be a better way to write that equation.

 

[jz92wjaz]

In probability, it looks like it would be written as 4 choose 2, meaning that you have 4 sentences and choose 2 of them. The equation gives the number of unique results (ab is the same as ba). Google "Combination".

 

[ellipsis]

Hey, computer scientist here. Cool project you're working on. I stumbled across this pattern while messing around with tabular K-map simplification (boolean logic):

You have 4 variables (but this can be generalized to n variables) and are trying to find the total number of associative expressions such that AB = BA. (Looping through for A AND B as well as B AND A would be inefficient)

This problem is analogous to finding the number of lines between a given number of points (see below). The formula is
$$
\frac{n^2-n}{2}
$$

Send me a PM: I'd like to take a closer look at your logic calculator.

*plus sign changed to minus sign as per jz92's post

 

[jz92wjaz]

The general equation for evaluating the number of unique combinations when you select k items from a set of n items is:

$$
\frac{n!}{(n-k)!*k!}
$$

n choose 2 is
$$
\frac{n!}{(n-2)!*2!}
$$
Simplified, it is:
$$
\frac{n^2-n}{2}
$$

Comparing each combination of 2, where there are 4 sentences, comes out to a total of (16-4)/2, or 6 comparisons. This, of course, requires that the loops are set up in a way that you never test the same combination twice.