bobmerhebi
- 38
- 0
Double Atwood Machine: relation between the contraints & the variables ?!
Hello. I am taking an analytical mechanics course & there's 2 "simple" equations relating the constraints to the variables. The problem is actually a class example. Here is it
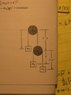
1. The figure of the example is attached.
We are supposed to find the Lagrangian L = T-V, but I was stuck at correctly proving the following (for which I am asking for help in proving). I should note that I was able to find L & the equations of motion by altering the figure & making use of the height of the masses relative to (my) chosen reference.:
(x2 + x1) - l =0 && (2x1 + x2 + x3) - (2l + l') =0
2. NO Relevant equations: simple arithmetic
3. The Attempt at a Solution :
Apparently l = xp + x (though another element should be added -- can you tell me why this cannot be added ? -- & that is: \pi a, where a is the radius of the pulley).
Moreover,
x3 = (l' - x') + xp = (l + l') - (x1 + x')
Hello. I am taking an analytical mechanics course & there's 2 "simple" equations relating the constraints to the variables. The problem is actually a class example. Here is it
1. The figure of the example is attached.
We are supposed to find the Lagrangian L = T-V, but I was stuck at correctly proving the following (for which I am asking for help in proving). I should note that I was able to find L & the equations of motion by altering the figure & making use of the height of the masses relative to (my) chosen reference.:
(x2 + x1) - l =0 && (2x1 + x2 + x3) - (2l + l') =0
2. NO Relevant equations: simple arithmetic
3. The Attempt at a Solution :
Apparently l = xp + x (though another element should be added -- can you tell me why this cannot be added ? -- & that is: \pi a, where a is the radius of the pulley).
Moreover,
x3 = (l' - x') + xp = (l + l') - (x1 + x')
Attachments
Last edited: