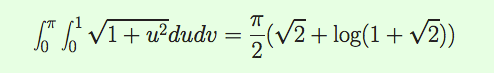SUMMARY
The discussion focuses on solving a double integral related to the surface area of a parametric surface. The user successfully computed the cross product but struggled with the double integral. The solution provided involves evaluating the integral as follows: $$\int_0^{\pi}\ \int_0^1\sqrt{1+u^2}du\ dv=\pi \int_0^1\sqrt{1+u^2}du$$, indicating that the inner integral simplifies to a constant, allowing for straightforward evaluation of the outer integral.
PREREQUISITES
- Understanding of double integrals in calculus
- Familiarity with parametric surfaces
- Knowledge of cross product calculations
- Basic integration techniques
NEXT STEPS
- Study the properties of double integrals in multivariable calculus
- Learn about parametric equations and their applications in surface area calculations
- Explore techniques for evaluating integrals involving square roots
- Review the concept of surface area in relation to vector calculus
USEFUL FOR
Students and professionals in mathematics, particularly those studying calculus, multivariable calculus, and vector calculus, as well as anyone involved in computational geometry or surface area calculations.