Thiru07
- 41
- 0
Homework Statement
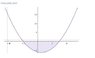
Given : (y+2)(y-3) <= 0
Homework Equations
The Attempt at a Solution
Now, I have y-3 <= 0 or y+2 <= 0
Hence, y <= 3 or y <= -2
But how
is correct?-2 <= y <= 3
I think
is wrong because y <= -2.-2 <= y <= 3
Can someone please clarify?