Aurelius120
- 269
- 24
- Homework Statement
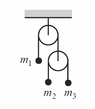
- In a double Atwood machine(pulley suspended from another pulley), a mass, m1 is suspended from one side of the upper pulley(on the other side is the lower pulley) and masses m2 and m3 are suspended from either side of the lower pulley. 𝑚3>𝑚2>𝑚1
𝑇 is the tension in the lower strings
𝑇1 is the tension in the upper strings
𝑎2 is the acceleration of 𝑚1 and of the lower pulley system (as a whole)
𝑎1 is the acceleration of 𝑚2 and 𝑚3 in the lower pulley (taking only the lower system into consideration)
𝑔 is the acceleration due to gravity
I want to find the net acceleration of each mass and the time for m1 to strike the upper pulley given the length of the string from m1 to the upper pulley is 20cm
- Relevant Equations
- N/A
I think the equations should be
𝑇−𝑚2𝑔=𝑚2𝑎1
𝑚3𝑔−𝑇=𝑚3𝑎1
𝑇1−𝑚1𝑔=𝑚1𝑎2
2𝑇−𝑇1=(𝑚2+𝑚3)𝑎2
P.S.- My textbook assumes T1 = 2T.
I don't understand why that is so.
𝑇−𝑚2𝑔=𝑚2𝑎1
𝑚3𝑔−𝑇=𝑚3𝑎1
𝑇1−𝑚1𝑔=𝑚1𝑎2
2𝑇−𝑇1=(𝑚2+𝑚3)𝑎2
P.S.- My textbook assumes T1 = 2T.
I don't understand why that is so.