-- E/M conceptual question regarding electric potential

Click For Summary

Discussion Overview

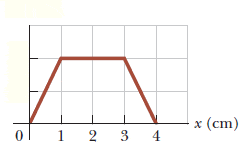
The discussion revolves around the relationship between electric potential (V) and electric field direction along the x-axis, particularly focusing on how the slope of a V(x) graph indicates the direction of the electric field. Participants explore concepts related to charge distributions and the behavior of test charges in electric fields.

Discussion Character

  • Conceptual clarification
  • Exploratory
  • Debate/contested

Main Points Raised

  • Some participants inquire about the implications of a negative or positive slope in a V(x) graph regarding the direction of the electric field.
  • One participant suggests considering charge distributions that could produce the described potential graph, mentioning hollow spheres and concentric conducting spheres.
  • There is a discussion about how a uniform electric field affects a positive test charge, with some participants asserting that the charge moves towards lower potential.
  • Participants explore the relationship between the slope of the potential graph and the direction of the electric field, with some concluding that a positive slope indicates a field pointing left and a negative slope indicates a field pointing right.
  • Questions arise about the definition of field direction and whether it is arbitrary, prompting clarification on how to specify direction with respect to the x-axis.

Areas of Agreement / Disagreement

While there is some agreement on the relationship between the slope of the potential graph and the direction of the electric field, the discussion includes varying interpretations and clarifications, indicating that multiple views remain on the specifics of the charge distributions and the implications of the slopes.

Contextual Notes

Participants reference specific scenarios and examples, such as hollow spheres and uniform fields, but do not resolve all assumptions or dependencies related to these examples.

momowoo
Messages
16
Reaction score
1
So in a graph where V is a function of x, when the slope is negative what does that mean about the direction of the field along the x axis? What about when the slope is positive?
SerPSE8-25-p-034.gif
 
Physics news on Phys.org
momowoo said:
So in a graph where V is a function of x, when the slope is negative what does that mean about the direction of the field along the x axis? What about when the slope is positive?
SerPSE8-25-p-034.gif
Welcome to the PF.

Can you think of a charge distribution that might cause that V(x) graph? You might also consider if conductors might be involved... :smile:
 
Would that be a hollow sphere?
 
momowoo said:
Would that be a hollow sphere?
That's not what I'm picturing, but perhaps it might work as well. But it would take multiple hollow concentric conducting spheres charged to different voltages, no?
 
How does the field relate to the potential difference? Say you had a uniform field point to the right. Imagine placing a positive test charge in that field. Which way will the field push the charge? Will a positive test charge tend to move towards higher or lower potential?
 
towards lower potential
 
Can you sketch the concentric conducting shells example that you alluded to? Can you label the shells with their voltages to make that graph work? :smile:
 
momowoo said:
towards lower potential
Exactly. So what does that tell you about your diagram?
 
ohhh so if the graph shows a positive slope then the test charge would be moving towards the positive charge and if its negative then it would be moving away?
 
  • #10
momowoo said:
ohhh so if the graph shows a positive slope then the test charge would be moving towards the positive charge and if its negative then it would be moving away?
Where the graph shows a positive slope, the positive test charge would tend to move towards lower potential (to the left). So what direction must the field be in that region?

So how does the field direction depend on the slope of the potential graph?
 
  • #11
How do you define field direction? Wouldn't saying left and right be arbitrary?
 
  • #12
momowoo said:
How do you define field direction? Wouldn't saying left and right be arbitrary?
Just specify the direction with respect to the x-axis given. ("To the right" corresponds to the +x direction, in this case.)
 
  • #13
ohhhhh. So in that case, the region defined by the positive slope is probably to the left of a positive test charge. The area in which there is a constant V value is at the charge and then the negative slope would be to the right of the test charge because there is lower PE the larger the x value.
 
  • #14
its like when x is equal to 0(the reference point) that is some distance to the left of the pos charge right?
 
  • #15
What's the direction of the field?
 
  • #16
To the left?
 
  • #17
So does this mean that a positive slope means moving to the left and neg slope means moving to the right?
 
  • #18
momowoo said:
To the left?
Yes. Where the potential rises to the right, the field points left.
 
  • #19
THANK YOU SO MUCH FOR HELPING ME <3
 
  • Like
Likes   Reactions: berkeman
  • #20
momowoo said:
So does this mean that a positive slope means moving to the left and neg slope means moving to the right?
Yes. The field is related to the negative (opposite) of the slope of the potential graph. So where the slope is positive, the field is negative -- pointing to the -x axis (to the left, in this case). And where the slope is negative, the field is positive.

momowoo said:
THANK YOU SO MUCH FOR HELPING ME <3
You are very welcome.
 

Similar threads

Undergrad Electric Potential in circuit
  • · Replies 3 ·
Replies
3
Views
1K
Undergrad Electric Potential -- Is my understanding correct?
  • · Replies 6 ·
Replies
6
Views
1K
Undergrad Work done by electric field of an irregularly shaped conductor
  • · Replies 3 ·
Replies
3
Views
2K
Graduate Electrical potential of a thin wire in an E field
  • · Replies 11 ·
Replies
11
Views
2K
Undergrad Is this example incorrect in Agawal's book on electric circuits?
  • · Replies 3 ·
Replies
3
Views
2K
Undergrad How Do Electric Potential, Potential Energy, and Work Interact in Physics?
  • · Replies 18 ·
Replies
18
Views
3K
Graduate Potential Energy of an Electric Dipole in a Uniform Field
  • · Replies 11 ·
Replies
11
Views
4K
High School Ion Trap and Time-Varying Potentials
  • · Replies 1 ·
Replies
1
Views
2K
Undergrad Help with understanding electric potential graphs
  • · Replies 2 ·
Replies
2
Views
5K
Undergrad Trying to better understand the physics of electrical earth ground
  • · Replies 18 ·
Replies
18
Views
4K