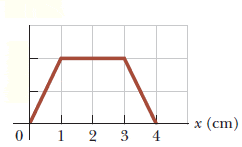
In a graph where electric potential (V) is a function of position (x), a negative slope indicates that the electric field points in the positive x-direction, while a positive slope means the field points in the negative x-direction. This relationship arises because the electric field is defined as the negative gradient of the potential. A positive test charge will move towards lower potential, which corresponds to the direction of the electric field. Thus, if the slope of the potential graph is positive, the field points left, and if the slope is negative, the field points right. Understanding this relationship is crucial for analyzing charge distributions and electric fields.