cmb
- 1,128
- 128
I know the basic equations of a solenoid carrying a current, the consequences of having an iron core inside one, and how that derives from Ampere's law. But these suggest that the only figure of merit is the cross section area of an iron core and the solenoid, not their shape.
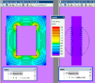
Thinking in more 'Newtonian' thoughts for cases in the real world of things with finite lengths and widths, if the cause of a magnetised domain inside a core is because of proximity to a magnetic field around the solenoid wires, then is the magnetic flux improved if the core is a thin flat bar rather than a circular cylinder, seeing as the 'centre' of a flat bar (of the same cross section area, of course) is closer to the solenoid wires than the centre of a cylindrical solenoid.
The expense for normal purposes, of course, is that more wire would be needed around a non-circular core, thus more power needed for the same current and wire cross section. So it is not a solution to a commercial problem (other than packaging, I suppose). But other than those disadvantages, are there any advantages to using a flat bar core such as improved flux for a given A/turn, or flux density, or saturation? Or is the flux worse too?
Thinking in more 'Newtonian' thoughts for cases in the real world of things with finite lengths and widths, if the cause of a magnetised domain inside a core is because of proximity to a magnetic field around the solenoid wires, then is the magnetic flux improved if the core is a thin flat bar rather than a circular cylinder, seeing as the 'centre' of a flat bar (of the same cross section area, of course) is closer to the solenoid wires than the centre of a cylindrical solenoid.
The expense for normal purposes, of course, is that more wire would be needed around a non-circular core, thus more power needed for the same current and wire cross section. So it is not a solution to a commercial problem (other than packaging, I suppose). But other than those disadvantages, are there any advantages to using a flat bar core such as improved flux for a given A/turn, or flux density, or saturation? Or is the flux worse too?