Magnetic Field outside an Iron Core Solenoid

[Chadvad]

I need help in calculating the magnetic field outside of an iron core solenoid at different distances.
I have made an electromagnet by taking a 99.99% pure iron (5cm in length and 1 mm in radius) and wrapping wire over it. I have measured it's magnetic field at the end and cannot find an equation from literature (Biot -Savart) that accurately models the magnetic field as I move the gaussmeter farther from one end (referring to moving the instrument further along the z direction in the picture I uploaded).

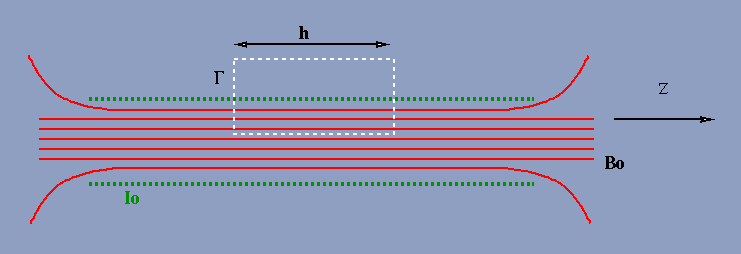
I know that the permeability of the iron is 2.5x10e-1 from a wikipedia chart on permeability
https://en.wikipedia.org/wiki/Permeability_(electromagnetism).

I have been using a formula that I found here, but does not seem to be working since it only applies to air core solenoids.

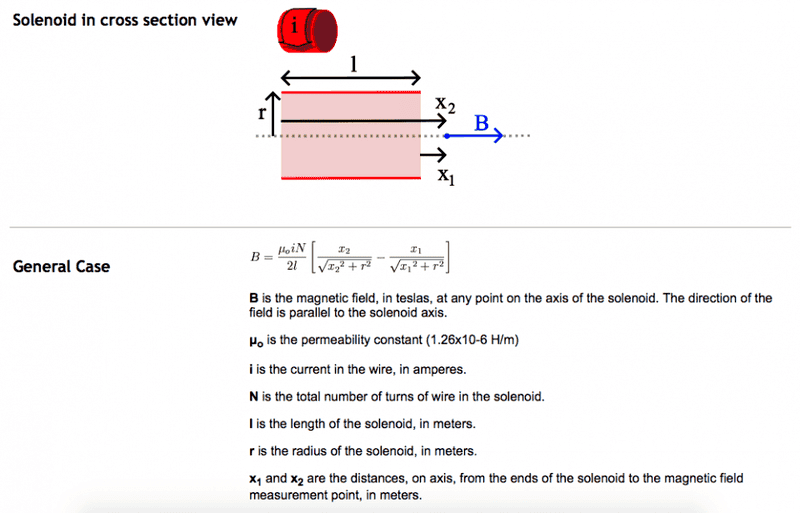
Does anyone have an idea on how I can more closely model/ create an equation for this relationship?
Thanks

 

[Charles Link]

Your equation, if I read it correctly is for a solenoid without the iron core. The magnetic field from the iron core, if the magnetization M is uniform, a good assumption, can be calculated from the surface current per unit length $K_m=M \times \hat{n}/\mu_o$ using Biot-Savart.($\hat{n}$ is outward pointing unit vector normal to the surface.) The surface currents have a geometry basically identical to those of a (finite length) solenoid, so any equations that work for a finite solenoid would also work for the field generated by the surface currents of the uniformly magnetized core. The magnetization $M$ can often be found from hysteresis curves (M vs. H ) where H is the field of the solenoid without the iron core.

 

[Chadvad]

Thanks!
I have a couple follow up questions.
How does this incorporate moving the sensor farther away on the z plane?
And how do I use a hysteresis curve, since there does not seem to be a standard one available online?

 

[Charles Link]

Thanks!
I have a couple follow up questions.
How does this incorporate moving the sensor farther away on the z plane?
And how do I use a hysteresis curve, since there does not seem to be a standard one available online?

I think the equation you have works for any solenoid of radius r and it works for anywhere along the z-axis, both inside and outside the solenoid. (This formula came up previously in a physics forums discussion, and I was able to derive it for the person who asked, does it work? The two terms with the x/sqrt( ) are cosines of angles and this formula containing cosines is often the formula given in E&M textbooks for a solenoid.) For the vector cross product $K_m=M \times \hat{n}/\mu_o$ the result is $K_m=M/\mu_o$. The $K_m$ replaces $Ni/L$ in the formula for $B$. This gives the iron core contribution. Use whatever radius $a$ that the iron core has (in place of "r") and whatever length. To be most accurate, the field from the solenoid gets added (superimposed) to that of the iron core. (The field from the iron core is normally many times larger.) M can also be computed from permeability numbers. $B=\mu H=\mu_o H+M$ where $H$ is the field from the solenoid without the core. The result of a little algebra is $M=(\mu-\mu_o)H$ and $H=B_1/\mu_o$ where $B_1$ is the $B$ field from the solenoid without the iron core. You will find considerable variations in the permeability $\mu$ for different materials as well as different types of iron.

 

[Charles Link]

Additional comment: The permeability $\mu$ varies considerably in different materials, and if I have read the different items correctly, the $\mu$ for reasonably good magnetic materials will cover a range from 100 to 1000 and more. The result is, if you have any kind of accuracy with your gaussmeter, you can probably generate a much more accurate value for $\mu$ than by selecting a number from a handbook. I would be interested in hearing if other readers concur, but I think this is the case. Unless you actually have a manufacturer's specification for a value they measured for the material, your own measurement is likely to give you a much more accurate number for $\mu$. I think even your almost pure iron sample can come in many different forms (with different $\mu$'s) including in a very uniform crystalline formation or in polycrystalline forms of varying degree. (More info. can probably be found about this in the literature somewhere. The sources on the subject that I have found don't spell this out in great detail.)