Guiding Magnetic Fields in Solenoid Coils: Design and Material Considerations

[artis]

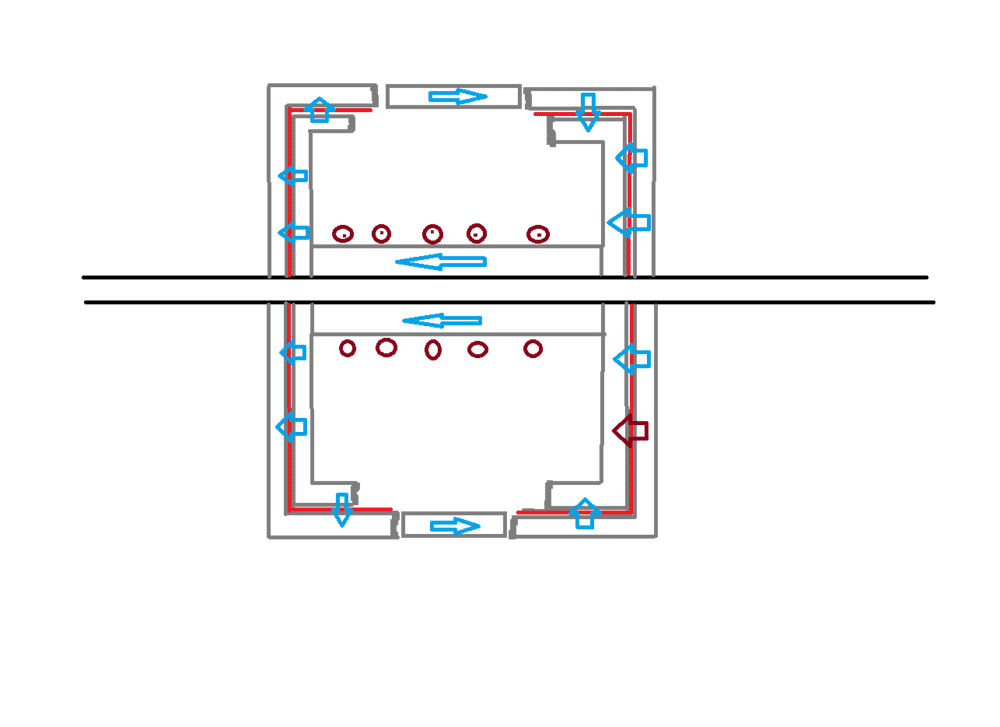
Hi, at this moment I'm trying to figure out one thing. I have a solenoid with a core that has an empty middle, the flux normally loops back around the outside of the solenoid to the other side where it enters back into the core. I need to route this field between the two ends of the solenoid core such that it passes through two gaps. I have made a crude paint drawing of how I would try to solve this can you please tell me whether my approach would work?
The field would be that of an 50/60hz AC current running in the solenoid coil , so a low frequency AC field.

There is one additional complication, ideally I would need the solenoid central endings to be joined by a material that has the same or close to the permeability of the solenoid core, but it's shape should cover the whole 360 degrees of a circle at the sides and a torus in the middle sections that close the flux path (seen in the picture as small grey rectangles) the torus part could be made from vertical stacked laminations but I can't figure out the side parts as they would need to be disc like but I cannot do it with laminations because each strip has the same width at both ends and so I would quickly run out of space near the center while there would be much empty space at the circumference.
Are there are large scale one piece (solid) materials that have the same or better characteristics than silicon steel or Metglas?

 

[essenmein]

Not sure what characteristics you are referring to when asking for "better", as far as I know in terms of Bsat at least, there is nothing that can support more flux density before saturation than silicon steel, typically ~1.7T, compare to metglass ~0.6T.

Is this going to be near your multi MHz thing?

 

[artis]

Well yes silicon steel is good in terms of saturation strength, the problem is the thin laminations are complicated to manage when one needs a non-standard form.

No it's not going to be near anything with high frequency, it's just a solenoid for low frequency AC , problem in this case is the shape that I need.
I'm still working on all of this including the other stuff, it ain't that easy.

 

[Baluncore]

I assume the hollow central core will saturate first. As the radius increases, so does the circumference. To maintain the same flux section, the saturation threshold of the material, and/or the thickness can be reduced. The outer cylindrical section can be quite thin.

 

[artis]

I guess what you are saying is that because there is more material available for the same amount of flux the outer portions won't saturate first instead for a given field strength the inner solenoid core around which the coil is wound would saturate first?

Well I did not draw this picture with scale and proportions in mind but as you said I could make the outer laminations thinner gaining space there and using that space to expand and make the central core (the one around the axis) thicker, larger diameter so that more material is there so that overall there would be equal cross sections of flux path both in the center and the returning outer toroid sections.

 

[artis]

While searching , I found something that is new or kind of new to me, a thing called shunt reactor and apparently some of them have cores that are disc shaped and made out of radial laminations.

http://www.encyclopedia-magnetica.com/lib/exe/detail.php/radially_laminated_core_-_magnetica.png?id=file:radially_laminated_core_-_magnetica.png

I wonder how could such radially laminated disc performing if I added a solenoid type cylindrical core to the inner diameter of the disc would the flux flow freely from the cylindrical laminations into the radial ones as per the model that I drew in the first post.
Only difference is that in my case the radial laminations would have an extended L shape in order to guide the field back around.

 

[Baluncore]

Why use laminations when you can use iron wire like on a "hedgehog transformer"?

Make a foam or wax temporary toroidal former. Wind it with iron wire so the outer surface has one full even layer. Coat it with epoxy. Mount it on a lathe for the rest of the process. Cut or grind the two gaps. Remove the one layer cylinder of epoxy-potted external wire from between the gaps, and put that aside. Remove the internal temporary former material. Spin the lathe to wind the copper wire solenoid onto the iron wire core, through the opening between the gaps. Restore the cylinder of iron wire between the gaps.

 

[essenmein]

Well yes silicon steel is good in terms of saturation strength, the problem is the thin laminations are complicated to manage when one needs a non-standard form.

No it's not going to be near anything with high frequency, it's just a solenoid for low frequency AC , problem in this case is the shape that I need.
I'm still working on all of this including the other stuff, it ain't that easy.

At 60Hz they don't need to be that thin, most transformers etc are what around half mm?

Then regarding shape, I would say the steel laminations are by far the easiest to do your self, cad up shapes -> CNC laser cut -> stack up desired core -> epoxy. It will be far more difficult to make custom shapes from metglass or ferrite.

One thing we've been looking at with curiosity is using powder iron (or Fe2O3) as filler in epoxy, now were were thinking injection molding, but you might be able to get enough powder into a two part resin and pour into a mold?

 

[artis]

the question is what would be the magnetic characteristics of such powdered iron made core, surely the fabrication sounds appealing and simpler which in itself is a good thing.

Well the more you live the more you learn, now I know about a hedgehog transformer , thanks to @Baluncore
Although simple but it won't cut my needs as I need a precise gap and everything would have to be sturdy enough to stand up to vibrations and other mechanical stresses.

Right now the best I can come up with is using laminations , for the central axis core simply use a rolled up sheet much like any toroid core uses just with a much smaller diameter and longer in length , aka a cylinder, then join the ends of such rolled cylinder with a disc at each end that consists of radial laminations (I'm seeing such are used in shunt reactor cores) only make the radial lamination to have an L shaped edge at the circumference where the field can turn 90 degrees in order to loop back as per my diagram

 

[artis]

I have a question, instead of making a radial disc by using this technique
http://www.encyclopedia-magnetica.com/lib/exe/detail.php/radially_laminated_core_-_magnetica.png?id=file:radially_laminated_core_-_magnetica.png

Could I simply use laminations that each extend from the inner diameter to the circumference but each gets thicker the longer it goes radially ?
Much like this

 

[Baluncore]

There is no advantage in using wedge shaped or thicker laminations. Skin effect in the lamination material will prevent the inside being used, so it just increases the weight. You need a dielectric paint or oxide, between the laminations of about 10% lamination thickness. That provides fast access for magnetic field to surface on both sides of all laminations. Magnetic field energy that diffuses more than one skin depth into the magnetic material cannot be recovered and so is lost as heat.

Since the magnetic section must be maintained, and there is no advantage in filling the gaps, you could twist each lamination through 90° as it radiates, so laminations end up edge to edge, or on echelon, at full radius. That way, the outer L bend does not have to be cut, it can be bent or folded.

 

[artis]

@Baluncore I agree that the wedge idea is a dead end just for the reasons you mentioned.
But could you expand on that last bit you said about twisting and turning the laminations as I did not exactly catch your thought.

The L shape would probably be rounded a bit instead of being with a sharp 90 degree cut because of other reasons that I need for this, I was just thinking each lamination could be cut into the L shape and then simply stacked together or maybe most of the laminations could be cut as U shapes in this way turned sideways they could both serve as the central axis solenoid core as well as join the outermost toroid ring, only some would have to be L shaped and put inbetween the U shapes at certain intervals to account for the wider area around the circumference than in the center.
Well this is just an idea. Having a rolled toroid in the center would be better from mechanical point of view.PS. can I use metallic end caps that join in the middle aka chassis in other words for any such piece of lamination as a structural part into which the lamination stack is mounted because such radial laminations have very low mechanical integrity compared to laminations found in an induction motor rotor for example or a toroid transformer.

 

[essenmein]

There is no advantage in using wedge shaped or thicker laminations. Skin effect in the lamination material will prevent the inside being used, so it just increases the weight. You need a dielectric paint or oxide, between the laminations of about 10% lamination thickness. That provides fast access for magnetic field to surface on both sides of all laminations. Magnetic field energy that diffuses more than one skin depth into the magnetic material cannot be recovered and so is lost as heat.

This is not quite correct, apologies if this seems nit picky!

The core is not intended to conduct current so the skin effect is not quite the phenomena involved, skin effect and core loss/effectiveness are driven by the same thing, ie eddy currents generated in conductive material by a changing magnetic field, frequency drives both the maximum usable wire size and the minimum effective lamination thickness. In a magnetic core this could all be avoided if someone could only discover a non conducting ferro magnetic material, while they're at it, make the Bsat higher.

Anyway, these currents are generated due to the voltages induced in conductive loops perpendicular to the axis of a changing magnetic field, and since its a closed conductive loop, they tend to act like a shorted turn making large currents, burning power and generating their own opposing magnetic field.

In a wire this field axis is the center of the wire, in a core this depends on how the flux is flowing. In a wire you have no way to change the axis of the field generated by the flowing current wrt the wire itself, and the resulting opposing field tends to push all the electron flow to the outside of the wire, all you can do is break the wire into lots of little wires that spend an equal amount per length in the center as they do the outside "forcing" the current to flow everywhere (Litz wire). In a core for the lamination to have any effect they must be parallel to the field axis, this alone will determine how they have to oriented in the core for them to do anything. For ferrite you don't care about orientation because its lots of little insulated balls of conductive magnetic material therefore the field axis is not relevant, ie ferrite is an isotropic material wrt magnetic fields, compared to a laminated core which is distinctly anisotropic.

Basically the laminations intent is to reduce the area of the conducting loops (frequency dependent!), reducing the induced current therefore reducing the power loss and the generated opposing field (ie high frequency roll off of the core permeability, as eddy currents block more field, permeability tends to that of free space). If there are no lamination its one large loop, which doesn't take much deltaB to generate large currents neutering the effective permeability of the magnetic core at very low frequencies. As you break up the core material into layers etc you have to prevent electrical conduction between the laminations, other wise nothing changes. So this insulation material does nothing other than prevent electrical conduction between layers, there is no prescribed minimum thickness other than "thou shalt not allow electrons to flow", I don't think the speed of the field is affected in any way.

This insulation does reduce the amount of magnetic material in the core volume as there is a practical limit to making thin functional insulation layers between sheets, therefore reducing the total flux you can carry per given x section area. The only thing that stops a magnetic field as far as I know is another magnetic field, so core "penetration" is prevented only by the induced eddy currents generating an opposing magnetic field which essentially cancels/reduces the total field inside the material, ie reducing the total magneto motive force on the domains inside therefore reducing the total generated flux density -> looks like frequency dependent permeability reduction and these currents make heat (attenuation is limited by the conductivity of the conducting material).

 

[essenmein]

View attachment 246433

So to build this the laminations have to be parallel to your arrows. The center part and the ring that connects the two outer disk things need to have the laminations length ways, so could be rolled out of foil like you said. The L shaped sections the arrows are not showing the full picture, the flux also has to travel down the L's and then turn 90deg to make it over the gap. I don;t think this is feasible to build out of sheet laminations, since the flux is basically wanting to flow in two axis. I assume the red line is some sort of electrically insulating air gap? Those L's would likely want to be tapered as the flux density tails off the further from the center you get on one and gets larger for the receiving one, increasing x area from increasing diameter may largely offset this. For the L's I think ferrite is your only feasible option.

 

[Baluncore]

This is not quite correct, apologies if this seems nit picky!

You are simply viewing it from a different position and direction. We cannot deny the loopy coupling of current with magnetic field. The thing we call skin effect is a symptom of the diffusion rate of fields and currents through a material.

You are ignoring the proximity effect of fields between the adjacent lamination surfaces in a core. A similar effect takes place between adjacent wire surfaces within a litz bundle. In both cases, the thickness of the insulation is important in separating the conductive surfaces sufficiently to allow quick access from outside the conductive bundle or magnetic core. That has been largely forgotten over the last 100 years as school students, electrical contractors and servicemen have been taught wrongly to think simply of electrical energy as flowing with the electrons, inside the wires, rather than as the poynting vector in the space between the conductors.

Laminations are utilised to make the full volume of the magnetic material quickly accessible to the field. We can select the lamination orientation to minimise peripheral eddy current loops, or we can select the orientation to guide the magnetic field along a specified path. Neither view is in itself complete, we must consider both at the same time.

 

[artis]

I guess the point @Baluncore is making can be also be said about wires and insulation , where different types of insulation have different dielectric properties and if run parallel can affect the AC current through the sum total of all the parallel wires.

Also could you explain what you meant in the second part of your post #11?

@essenmein , but why couldn't the flux travel upwards the inner L and as it does so also leak over to the outer L continuously because the inner L's outermost section is shorter and only the outer L is connected magnetically for the field to travel and loop back so the flux would tend to go in the outer L.
The gap between the two L shaped discs would be no more than few mm thick and filled with copper conductor.

 

[Baluncore]

Also could you explain what you meant in the second part of your post #11?

Start conceptually with a square bracket lamination. Bend the ends 90 deg. Twist the flat ends to point to the ends to the gap.
The thin laminations then sit close to each other in the core.
The width of laminations cover the outside diameter / circumference, and end at the gaps.
Together the twists in the legs nest together and look like a turbofan compressor from the end.

 

[Baluncore]

There are too many questionable points in your post, and your sentences are so complex that it is impossible to argue all the points. For that reason I present one only here.

As you break up the core material into layers etc you have to prevent electrical conduction between the laminations, other wise nothing changes. So this insulation material does nothing other than prevent electrical conduction between layers, there is no prescribed minimum thickness other than "thou shalt not allow electrons to flow", I don't think the speed of the field is affected in any way.

I believe you are disputing the requirement for ≈10% insulation thickness between laminations. So I will try to explain why such a wide layer is necessary between laminations.

Consider two adjacent laminations with insulation between them. Drawn in section, with the magnetic B field perpendicular to the page. Initially B passes through the insulation layer. As B diffuses into the surface boundary of the lamination, a peripheral current flows in the lamination surface. Notice that the current flows in the same sense in each lamination. Draw arrows on the periphery of both laminations to show current direction.

Notice how the current on both the sides of the lamination, and on the sides of the insulation, flow in opposite directions. Notice that with the B field direction, the energy is moving with B into the laminations from the faces on both sides. After time for diffusion, the currents meet and cancel on the mid-plane of the lamination, where the B fields are parallel and in the same direction. Everything is good, so long as the energy has not diffused in too deep, and so cannot be recovered in time. That distance is related to the skin depth in the lamination material. The boundary that prevents loss of energy is where the two opposite current sheets cancel at the mid-plane. B cannot begin to enter and diffuse through the conductive lamination without the peripheral current.

As insulation thickness approaches zero, the two opposite surface currents approach coincidence and so cancel. That prevents the magnetic field entering the lamination. In effect the insulation is so thin it has choked the entry of B into the lamination material.

 

[artis]

@Baluncore Hmm interesting, actually I have never thought about flux and laminations this way , I always thought that flux enters the thin end side of a lamination then travels along the lamination and exits at the other thin side, after all this is the reason why laminations can only be used in a certain angle as putting their flat sheet sides towards the flux would simply results in the first lamination developing large circular eddy currents blocking any field getting into the next sheet after the first one.

Could you also say that without insulation the lamination stack starts to look like that single sheet put in the direction of the field and so the smaller individual eddy currents turn into one larger and again oppose the field entry?
Sounds a bit like the reason why one chops up large firewood in small pieces so that the flame can penetrate also from the sides because we all know trying to burn a single large piece never works unless the fire is a raging inferno because the chunk is so large that the surface gets hot and almost repels the flame.

 

[artis]

As for the twisting that you suggest , I now understand but doesn't that totally defeat my plan of having a uniform flux direction in the gaps at each side between the L shapes?
In my drawing I'm simply having two L shaped laminations stacked in a disc put on each side on a single central lamination that has L shaped sides but in theory could be cut out of single sheet as one piece but the idea is that the gap is always faced by the thin side of the lamination not the flat sheet side otherwise how would the flux (show by pink arrows this time) get through the gap from central lamination to the outer one?

 

[essenmein]

I believe you are disputing the requirement for ≈10% insulation thickness between laminations. So I will try to explain why such a wide layer is necessary between laminations.

Yeah, disputing the requirement for a minimum thickness from a magnetic perspective.

Consider two adjacent laminations with insulation between them. Drawn in section, with the magnetic B field perpendicular to the page. Initially B passes through the insulation layer. As B diffuses into the surface boundary of the lamination, a peripheral current flows in the lamination surface. Notice that the current flows in the same sense in each lamination. Draw arrows on the periphery of both laminations to show current direction.

I'm curious to drill a little deeper here, I'm pretty certain electricity only works in one way, and that way is the same for both of us. Maybe its a difference in terminology? Don't know, but I'll post where I have issues with this paragraph and see? Rather than the whole thing might get to the bottom of it easier.

"Initially B passes through insulation layer"

B as I understand it is flux density, which is typically described using a vector field indicating the intensity and direction of the force a charged particle of 1C moving at 1m/s would experience the instant it was located at a specific place (Tesla = N/A-m). B is not a substance that moves, "passes through insulation layer" etc. When we plot field lines, the lines appear to move, but the lines are simply indicating the contour where one value of intensity exists (say 0.5T), as something changes, the location that was previously exerting 0.5N/A-m might now exert 0.6N/A-m. So a moving field line indicated intensities have changed, not that a material substance has moved or passed through anything. Using field lines is a mathematically convenient way to talk about electrical laws but I'm not sure talking about how many field lines you cross is really conveying what is happening. When you cross a large number of B field lines you have a large gradient of flux density per time, ie delta B is large, and it is the rate of change of force intensity on charged particles that is the important quantity, not this moving line construct that we use to represent these forces."As B diffuses into the surface boundary of the lamination, a peripheral current flows in the lamination surface."

As mentioned above, flux density is a description of the intensity and direction of force exerted on a charge, how can these values of forces "diffuse" into anything? This doesn't make sense to me.

In the context of a magnetic core, the ferro magnetic material responds to an external H field by the relation H=uB to produce a force intensity B, in free space B and H are the same except for a unit difference, but in a magnetic core the materials magnetization contributes, so in my view of this 2D lamination you drew up there B is not moved or diffused, but "created" inside the material as it responds to an external H field* and would only pass through air gaps in plane with the page. The B that would be present in the insulation is not zero, but much smaller than that in the core (by ratio of relative permeability of the material).

*H field is also vector field, describing the intensity and direction of magneto motive force, A/m, this is an odd unit, its quite small. 1 A/m is the MMF produced by 1A flowing in 1 turn of wire around a magnetic core with a core length of 1m.

Now I completely agree that the instant any intensity changes, you get rate of change of those values all together behaving according to Maxwells equations (lets ignore relativity here lol), changing flux density induces voltages, those voltages produce electric fields, those voltages create currents which create their own opposing magnetic fields which now create vector force summations everywhere these two vector fields meet, resulting in a new intensity and direction of those forces.

I struggle with the description of field quantities as moving through things and diffusing, these are terms to me at least reserved for physical stuff, diffusion is for example quite appropriately used to describe how a gas fills a room. I did a quick search on "diffusion of magnetic fields" and the only thing that came up is various things about plasma diffusion in a magnetic field, which does make sense.

 

[Baluncore]

As for the twisting that you suggest , I now understand but doesn't that totally defeat my plan of having a uniform flux direction in the gaps at each side between the L shapes?

You have not identified the relative motion of the different parts, nor what your device is supposed to do, or how it is expected to work. All we have is a sectional diagram that you understand. If by omitting critical information you minimise the question, then you can expect the quality of the answers to also be minimised.

Many creative experts with a lifetime of experience have worked in the field of electromagnetic machines. 1. What makes you think that someone without experience will stumble across some useful device that has been missed by all who have gone before? 2. How do you know you are not actually deluded? 3. Why do you try to create a final design that will require extensive tooling, before you have a numerical simulation model, or a crude prototype that actually demonstrates it might really work as you hope?

 

[artis]

I'm leaving out information simply due to this being an internet forums, if I included everything we could write a book here(that no one would like to read) and I would be nowhere closer to what I want to understand. At least my experience has been over the years that shorter posts get more answers than long ones.

Maybe I am deluded, but so far everything agrees with physics it's just the shape of things that's complicated.

I was just interested is it possible to have such a homogeneous field in a circular disc shaped airgap, I will make some simulations both on this and other things that I have made,