- #1
IgorMele
- 1
- 0
Hello.
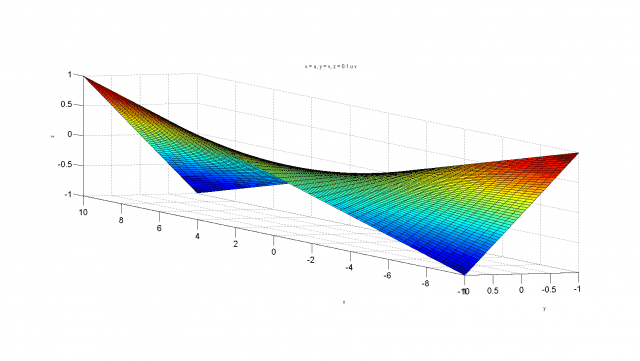
I would like to numerically determine eigenvalues of a rectangular membrane
which is twisted for [tex]\frac{\pi}{2}[/tex]. Example picture:
I'm solving Helmholtz equation:
[tex]\nabla^2u+k^2u=0[/tex]
where [tex]u=u(x,y)[/tex] and
[tex]\nabla^2 u=\frac{\partial^2u}{\partial x^2}+\frac{\partial^2v}{\partial y^2}[/tex]
If we write in matrix form:
[tex]-Au=k^2u=\lambda u[/tex]
[tex]A[/tex] is sparse matrix, which we get from second order finite difference approximation, [tex]\lambda[/tex] are eigenvalues. Analytical solution for rectangular membrane [tex]a\times b[/tex] is:
[tex]\lambda = h^2\pi^2\left(\frac{m^2}{a^2}+\frac{n^2}{b^2}\right)[/tex]
[tex]h[/tex] is distance between two points in a grid.
Here is solution for second mode:
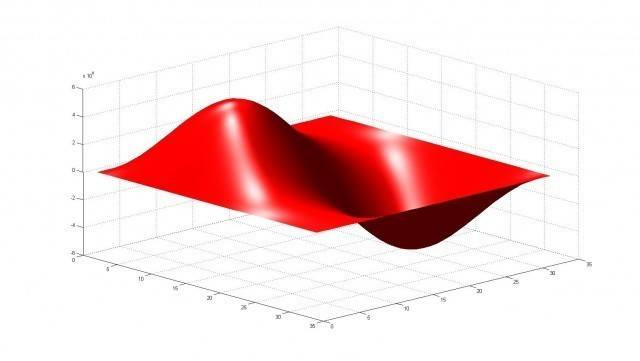
This was for normal membrane, now question is, what happens with eigenvalues when we twist membrane. Shape of membrane in parametric form:
[tex]x=u[/tex]
[tex]y=v[/tex]
[tex]z=uv[/tex]
[tex]u,v\in [-1,1][/tex]
or perhaps:
[tex]x=u[/tex]
[tex]y=v[/tex]
[tex]z=(u-1)(v-1)[/tex]
[tex]u,v\in [0,2][/tex]
In this way, we don't have negative [tex]u[/tex] and [tex]v[/tex]. In this case parametrization applies only for quadratic membrane, in equations should be also [tex]a[/tex] and [tex]b[/tex], but it's not so relevant. I will add them later.
Here I'm stuck. I don't know, how to write Helmholtz equation for this parametrization.
Any tip or help would be appreciated.
I would like to numerically determine eigenvalues of a rectangular membrane
which is twisted for [tex]\frac{\pi}{2}[/tex]. Example picture:
I'm solving Helmholtz equation:
[tex]\nabla^2u+k^2u=0[/tex]
where [tex]u=u(x,y)[/tex] and
[tex]\nabla^2 u=\frac{\partial^2u}{\partial x^2}+\frac{\partial^2v}{\partial y^2}[/tex]
If we write in matrix form:
[tex]-Au=k^2u=\lambda u[/tex]
[tex]A[/tex] is sparse matrix, which we get from second order finite difference approximation, [tex]\lambda[/tex] are eigenvalues. Analytical solution for rectangular membrane [tex]a\times b[/tex] is:
[tex]\lambda = h^2\pi^2\left(\frac{m^2}{a^2}+\frac{n^2}{b^2}\right)[/tex]
[tex]h[/tex] is distance between two points in a grid.
Here is solution for second mode:
This was for normal membrane, now question is, what happens with eigenvalues when we twist membrane. Shape of membrane in parametric form:
[tex]x=u[/tex]
[tex]y=v[/tex]
[tex]z=uv[/tex]
[tex]u,v\in [-1,1][/tex]
or perhaps:
[tex]x=u[/tex]
[tex]y=v[/tex]
[tex]z=(u-1)(v-1)[/tex]
[tex]u,v\in [0,2][/tex]
In this way, we don't have negative [tex]u[/tex] and [tex]v[/tex]. In this case parametrization applies only for quadratic membrane, in equations should be also [tex]a[/tex] and [tex]b[/tex], but it's not so relevant. I will add them later.
Here I'm stuck. I don't know, how to write Helmholtz equation for this parametrization.
Any tip or help would be appreciated.