Elastic Collision 4: Final Velocities

[Karol]

Homework Statement

Two identical masses collide. one is at rest. what are their final velocities.

Homework Equations

The relative velocities before and after the collision are identical:
$v_1-v_2=-(u_1-u_2)$

The Attempt at a Solution

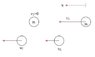
I draw the final velocities in the same direction:
$$\left\{ \begin{array}{l} mv_1=mu_1+mu_2 \\ -v_1=-(u_1-u_2) \end{array} \right.$$
It gives $$u_2=0$$ which isn't true, u₁ should be 0.
And more, i can switch between u₁ and u₂ in the drawing and it will also be good since they are drawn in the same direction, so, how do i know who stops?
I get this answer also if i use the conservation of energy formula instead of the relative velocities formula.
If i draw u₁ backwards and change the formula in accordance:
$\left\{ \begin{array}{l} mv_1=mu_1-mu_2 \\ -v_1=-(u_1-u_2) \end{array} \right.$
I again get the same result: $$u_2=0$$
Apart from the question i posed, do i have to assume a direction and then write the formuls accordingly or i have always to write:
$\left\{ \begin{array}{l} mv_1=mu_1+mu_2 \\ -v_1=-(u_1-u_2) \end{array} \right.$

 

[Doc Al]

The Attempt at a Solution

I draw the final velocities in the same direction:
$$\left\{ \begin{array}{l} mv_1=mu_1+mu_2 \\ -v_1=-(u_1-u_2) \end{array} \right.$$

The left hand side of the second equation should be $v_1$, not $-v_1$.

 

[Karol]

--

Thanks, it solved it.
I used the next set of equations:
$$\left\{ \begin{array}{l} mv_1=mu_1+mu_2 \\ \frac{1}{2}mv^2_1=\frac{1}{2}mu^2_1+\frac{1}{2}mu^2_2 \end{array} \right.$$
$\Rightarrow \left\{ \begin{array}{l} v_1=u_1+u_2 \\ v^2_1=u^2_1+u^2_2 \end{array} \right.$
I isolated u₁:
$\Rightarrow v^2_1=(v_1+u_2)^2+u^2_2$
And got the same answer, good. but when i solved the same set of equations by isolating v₁ i got a different answer:
$(u_1+u_2)^2=u^2_1+u^2_2 \rightarrow u_1 u_2=0$
Do you know this behavior of sets of equations, that you get different answers by using different ways?

 

[Orodruin]

No, you will not get different answers by doing it different ways. The statement $u_1 u_2 = 0$ simply tells you that either $u_1$ or $u_2$ is zero after the collision, both of which are perfectly valid roots ($u_2 = 0$ corresponds to the balls not having collided yet).

The equations you have are symmetric in $u_1$ and $u_2$ so if $u_1 = 0, u_2 = U$ is a solution, then also $u_1 = U, u_2 = 0$ must be a solution.

 

[Doc Al]

I used the next set of equations:
$$\left\{ \begin{array}{l} mv_1=mu_1+mu_2 \\ \frac{1}{2}mv^2_1=\frac{1}{2}mu^2_1+\frac{1}{2}mu^2_2 \end{array} \right.$$
$\Rightarrow \left\{ \begin{array}{l} v_1=u_1+u_2 \\ v^2_1=u^2_1+u^2_2 \end{array} \right.$

Realize that these equations are equivalent to those you used earlier.

I isolated u₁:
$\Rightarrow v^2_1=(v_1+u_2)^2+u^2_2$
And got the same answer, good.

You made an error in your substitution. $u_1 \ne v_1+u_2$.

but when i solved the same set of equations by isolating v₁ i got a different answer:
$(u_1+u_2)^2=u^2_1+u^2_2 \rightarrow u_1 u_2=0$

This time you did it correctly.

Do you know this behavior of sets of equations, that you get different answers by using different ways?

Only when you make an error.