Elastic Collision: Max Potential Energy Stored

[karis]

Homework Statement

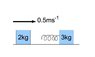
The figure shows a 2kg block moving at a speed of 0.5ms^-1 on a smooth horizontal surface. It collides head-on elastically with an initially stationary block of mass 3kg which is fitted with a light spring. What is the maximum elastic potential energy stored in the spring during collision?
A. 0.10J
B. 0.15J
C. 0.25J
D. It cannot be found as the force constant of the spring is not known.

Homework Equations

The Attempt at a Solution

if i treated the collision as an elastic one, i can't get the velocity of the two blocks, (i used the method of conservation of momentum)

Thank you! =)

 

[Delphi51]

This is a very interesting and difficult question!
I don't know how to do it.
If you use KE before = KE after, you get a second equation and can solve the pair of them for the the velocities of both carts after the collision. But this doesn't seem to help.

As the first cart contacts the spring on the second, there will be a force on both carts. The spring will compress and the force will increase (F = kx) until . . . . .
Answer that question and we'll have a grip on the problem!

 

[Delphi51]

I've been working on this for quite a while. I actually found a way to solve it using a system of 3 equations and then getting the maximum on a quadratic equation for the compression of the spring. I didn't get one of the choices given in the question. I also did it with a spreadsheet model and got the same answer. Kind of interesting! I would sure like to hear what the correct solution is.

 

[ideasrule]

This isn't a difficult problem. Two things are conserved: momentum and energy. At the moment of maximum compression, the two blocks have to be moving at the same speed; if they weren't, the spring would either stretch or continue to compress. With the conservation of momentum equation you can get this speed; with this speed you can calculate how much energy must be stored away in the spring.

 

[karis]

thanks so much!=]
i keep on calculating their velocities coz i thought they're different
but i got it now!

btw, the correct answer is 0.15J

 

[Delphi51]

Thanks, ideas! I actually figured that out in the middle of the night - and found the error in my spreadsheet this morning.