Swan
- 16
- 0
*URGENT* Elastic potential energy with box going up an incline.
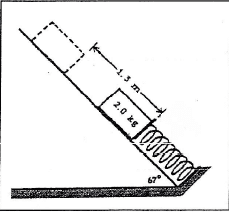
A spring having a force constant of 240 \frac{N}{m} is placed on a plane inclined at 67° to the horizontal. The spring is compressed 0.40 m and a 2.0 kg mass is placed on it. The coefficient of kinetic friction along the inclined surface is 0.53. Find the speed of the mass after it moves 1.3 m up the plane (above the completely extended spring).
Diagram
FN = m*g*cosθ
Ff = μ*FN
W = F*Δd
ET1 - Wf = ET2
Let H represent the height off the ground. Let h represent height between the boxes.
V1 = 0. So initial kinetic energy is negligible.
h = (sin67°)(1.3m + 0.4m)
Wf = Ff * (1.3m + 0.4m)
Wf = 6.9J
ET1 - Wf = ET2
mgH + \frac{1}{2}k*x2 - Wf = mg(h+H) + \frac{1}{2}mV22
mgH + \frac{1}{2}k*x2 - Wf = mgH + mgh + \frac{1}{2}mV22
**Both mgH cancel out on each sides**
\frac{1}{2}(240\frac{N}{m})(0.4m)2 - 6.9J = [(2kg)(9.8m/s2)(sin67°)(1.3m + 0.4m)]+ \frac{1}{2}(2kg)V22
I worked it out but I'm receiving an error. What am I doing wrong?
Homework Statement
A spring having a force constant of 240 \frac{N}{m} is placed on a plane inclined at 67° to the horizontal. The spring is compressed 0.40 m and a 2.0 kg mass is placed on it. The coefficient of kinetic friction along the inclined surface is 0.53. Find the speed of the mass after it moves 1.3 m up the plane (above the completely extended spring).
Diagram
Homework Equations
FN = m*g*cosθ
Ff = μ*FN
W = F*Δd
ET1 - Wf = ET2
Let H represent the height off the ground. Let h represent height between the boxes.
The Attempt at a Solution
V1 = 0. So initial kinetic energy is negligible.
h = (sin67°)(1.3m + 0.4m)
Wf = Ff * (1.3m + 0.4m)
Wf = 6.9J
ET1 - Wf = ET2
mgH + \frac{1}{2}k*x2 - Wf = mg(h+H) + \frac{1}{2}mV22
mgH + \frac{1}{2}k*x2 - Wf = mgH + mgh + \frac{1}{2}mV22
**Both mgH cancel out on each sides**
\frac{1}{2}(240\frac{N}{m})(0.4m)2 - 6.9J = [(2kg)(9.8m/s2)(sin67°)(1.3m + 0.4m)]+ \frac{1}{2}(2kg)V22
I worked it out but I'm receiving an error. What am I doing wrong?