Bashyboy
- 1,419
- 5
Homework Statement
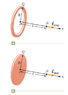
Assume a uniformly charged ring of radius R and charge Q produces an electric field Ering at a point P on its axis, at a distance x away from the center of the ring. Now the same charge Q is spread uniformly over a circular area the ring encloses, forming a flat disk of charge with the same radius. How does the Edisk produced by the disk at P compar with the field produced by the ring at the same point?
(a) Edisk < Ering
(b) Edisk = Ering
(c) Edisk > Ering
(d) Impossible to determine
Homework Equations
The Attempt at a Solution
My first suspicion was, that Edisk > Ering was the correct answer. This was so, because the disk can be thought of as many rings of infinitesmal size concentric. One infinitesmal ring would contribute to the electric field that is directed co-axially. This co-axial would begin to compound as you considered the remaining infinitesmal rings that constitute the entire disk.
Here is where came to a hault:
As you consider infinitesmal rings further from the center of disk, the angle that the infinitesmal ring makes with the x-axis becomes greater, thereby causing the co-axial component fo the electric field to dimish, as you move from the center of the disk.
In addition, I have this conjecture that the answer would also somehow depend on the relative of magnitude of x and R.
Could someone help me?