SUMMARY
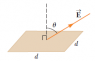
The correct calculation for electric flux through a surface with an electric field of 375 N/C, an angle of 64.2°, and a distance of 4.70 cm involves using the formula EAcosθ. The user initially calculated the flux as 0.167 N·m²/C, which was incorrect due to a calculator mode error. The accurate calculation yields a flux of approximately 0.3605 N·m²/C when using the correct angle in degrees and the proper distance conversion.
PREREQUISITES
- Understanding of electric flux and its calculation using the formula EAcosθ
- Familiarity with trigonometric functions, specifically cosine
- Knowledge of unit conversions, particularly from centimeters to meters
- Experience with scientific calculators and their mode settings (degrees vs. radians)
NEXT STEPS
- Review the concept of electric flux in electromagnetism
- Learn about the implications of angle measurement in calculations
- Practice unit conversion techniques, especially for electric field calculations
- Explore common calculator settings and how they affect mathematical computations
USEFUL FOR
Students studying electromagnetism, physics educators, and anyone involved in solving problems related to electric fields and flux calculations.