Electric flux through ends of an imaginary cylinder

[vcsharp2003]

Homework Statement

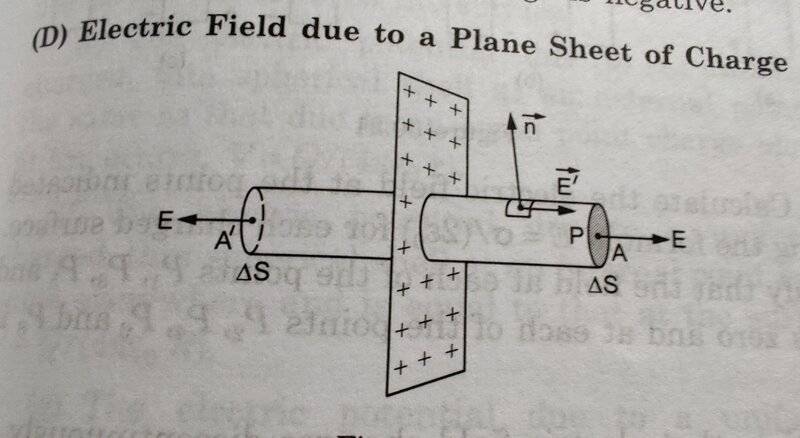
Imagine a cylinder that is symmetrical about an infinite plane sheet of charge as shown in the diagram. What is the electric flux through the ends $A \text{ and } A^{'}$ of this imaginary cylinder if $\Delta {S}$ is the area of each of these ends?

Relevant Equations

$\phi_E = \oint \vec E \cdot \vec {dS}$, which is the definition of electric flux

When I look at this question, I can see two possible values of electric flux depending on how I take the normal area vector for either ends $A \text{ and } A^{'}$.
What is wrong with my logic below where I am ending up with two possible answers? The book mentions that only $2E\Delta{S}$ is correct.

We know that electric field will be the same at each and every point on $A \text{ and } A^{'}$due to the symmetry of charge distribution on the plane sheet and it will always be perpendicular to $A \text{ and } A^{'}$.

So, let's assume that this electric field at every point of these surfaces is E.
Now consider an infinitesimal area $dS$ on each of these surfaces.
Then electric flux through $A$ could be one of the two values since the normal area vector could be either towards the infinite plane sheet or away from the sheet: $\phi_E = \oint \vec E \cdot \vec {dS} = \oint E dS \cos{0} \text{ , } \oint E {dS} \cos{2\pi}$
So, electric flux through $A$ could be either $E\Delta{S}$ OR $-E\Delta{S}$. The minus sign in second value is because $\cos{2\pi} = -1$

From above it follows that electric flux through the ends $A \text{ and } A^{'}$ could be $2E\Delta{S}$ or $0$. But the answer given is the first value and not the second value.

 

[BvU]

Hi,

Don't see no diagram...
You sure you don' t have your signs mixed up?

$\$

 

[vcsharp2003]

Hi,

Don't see no diagram...
You sure you don' t have your signs mixed up?

$\$

Sorry, I was busy in correcting latex part of my question. I am about to upload the diagram in a minute.

 

[vcsharp2003]

You sure you don' t have your signs mixed up?

No, I don't think so. Based on which direction I take the area vector of $A \text{ or } A^{'}$, I will get two different answers.

 

[TSny]

When calculating the flux through a closed surface, the direction of the area vector $\vec{dS}$ is always taken to be in the "outward" direction, i.e., away from the region enclosed by the surface.

 

[vcsharp2003]

When calculating the flux through a closed surface, the direction of the area vector $\vec{dS}$ is always taken to be in the "outward" direction, i.e., away from the region enclosed by the surface.

I get that, but in this question the flux through the ends is being separately calculated. We could just as well have two circular surfaces $A \text{ and } A^{'}$ rather than a cylinder.

 

[TSny]

I get that, but in this question the flux through the ends is being separately calculated. We vould just as well have two circular surfaces A \text{ and } A^{'} rather than a cylinder.

OK. In that case, if you're allowed to choose the directions of the area vectors arbitrarily for the two ends of the cylinder, then there is not a definite answer. You could get answers of $+2E\Delta S, -2E\Delta S$ or $0$. But then you might wonder why they even bother to mention the cylinder. They could have just given you the two circular areas.

The book's answer apparently corresponds to thinking of the two circular areas as part of a closed surface and therefore chooses the directions of the area vectors according to the convention for closed surfaces.

 

[vcsharp2003]

OK. In that case, if you're allowed to choose the directions of the arrow vectors arbitrarily for the two ends of the cylinder, then there is not a definite answer.

You're right. Since the diagram shows an imaginary cylinder so we need to consider it as a closed surface and then what you say about area vector pointing away from the closed surface makes sense.